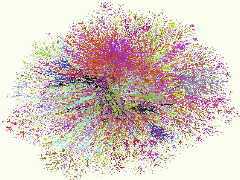
Figures: Quelques exemples de modes de visualisations de très grands graphes.
Remarque: Je suis en mission scientifique en Suède du 6 avril au 10 mai 2003. Les étudiants intéressés par un de mes sujets de mémoire peuvent me contacter par email durant cette période (blondel@inma.ucl.ac.be), ou convenir d'un rendez-vous après le 10 mai.
Cette page se trouve à l'adresse: http://www.inma.ucl.ac.be/~blondel/tfe2003.html
Comment visualiser de très grands graphes?
La visualisation de très grand graphes et réseaux tels que ceux du web ou d'un réseau de mobilophonie (de l'ordre du million ou du milliard de sommets) pose des problèmes théoriques et d'implémentation nouveaux. Dans le cadre de ce mémoire on analysera certaines méthodes de visualisation introduites récemment, on en proposera d'éventuelles extensions et on mettra en oeuvre un algorithme de visualisation.

Figures: Quelques exemples de modes de visualisations de très grands
graphes.
Codes, séquences binaires et rayon spectral conjoint
On s'intéressera dans ce mémoire à un problème en théorie des codes qui fait apparaitre la notion récemment introduite de rayon spectral conjoint d'un ensemble de matrices. Le problème est celui de la recherche du nombre maximum de séquences binaires de longueur donnée dont les différences évitent un ensemble de motifs interdits.
La différence entre deux séquences binaires de longueur n est une séquence de n caractères pris dans {-1, 0, +1}. Etant donné un ensemble fini D de séquences interdites de {-1, 0, +1}, le plus grand nombre de séquences binaires de longueur n dont les différences n'incluent aucun élément de D est donné par d(n). Les auteurs de l'article [1] on démontré que la limite d(n)^(1/n) existe et peut être caractérisée au moyen du rayon spectral conjoint de matrices construites au départ de l'ensemble D.
Le rayon spectral conjoint de matrices est en général NP-difficile a calculer [2]. Les matrices construites dans [1] ont toutefois une structure particulière pour laquelle il n'est pas exclu de trouver des algorithmes polynomiaux. Dans le cadre de ce mémoire on analysera d'abord le degré de généralité de l'algorithme proposé dans [1] et on analysera ensuite plus finement la complexité algorithmique du problème proposé. On tentera en particulier de déterminer si le problème est ou n'est pas NP-difficile.
Références.
[1] B. Moision, A. Orlitsky, and P. Siegel, On codes that avoid specified differences,
IEEE Transactions on Information Theory, 47:1, pp. 433-442. Disponible au départ
de http://ece.ucsd.edu/~alon/pub.html
[2] J. Tsitsiklis, V. Blondel, The Lyapunov exponent and joint spectral
radius of pairs of matrices are hard -- when not impossible -- to compute and
to approximate, Mathematics of Control, Signals, and Systems, 10, pp. 31-40,
1997. Disponible au départ de http://www.inma.ucl.ac.be/~blondel/publications/
Coordination d'agents autonomes
Pour les amateurs de (fort belles) animations, voir le site: http://www.red3d.com/cwr/boids/ qui illustre certain des aspects que nous souhaitons développer dans ce mémoire.
Des particules (ou des "agents") se déplacent de manière autonome dans le plan. Les vitesses de déplacement des agents sont constantes et sont toutes identiques. Les directions de déplacement sont mises à jour périodiquement et simultanément pour tous les agents en suivant une règle simple: la nouvelle direction d'un agent est donnée par la moyenne des directions de déplacement de ses voisins immédiats.
Des simulations montrent qu'en obéissant à une telle règle d'évolution locale les agents finissent par tous se déplacer dans la même direction, et ce malgré le fait que l'ensemble des plus proches voisins d'un agent peut évoluer dans le temps. Une base théorique a été proposée récemment pour expliquer ce phénomène et nous proposons dans le cadre de ce mémoire d'analyser la validité de la justification proposée et d'en identifier les limites.
Références.
T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, O. Shochet and A. Tenenbaum,
Novel type of phase transition in a system of self-driven particles, Phys. Rev.
Lett. 75:1226-1229 (1995).
A. Jadbabaie, J. Lin, and A. S. Morse, Coordination of Groups of Mobile Autonomous
Agents Using Nearest Neighbor Rules, IEEE Transactions on Automatic Control,
submitted 2002. Disponible au départ de: http://entity.eng.yale.edu/controls/publications.html
Lindemayer systems
L-systems are a mathematical formalism proposed by the biologist Aristid Lindenmayer in 1968 as a foundation for an axiomatic theory of biological development. The central concept of L-systems is that of rewriting. Rewriting is a technique for defining complex objects by successively replacing parts of a simple initial object using a set of rewriting rules or production. L-systems have found several applications in computer graphics and have been extensively studied as devices for defining languages. They are also intimately related to a number of classical mathematical objects.
In this project, we will investigate the connections between L- and D0L-systems with the classical, and so far unsolved, Pisot problem in number theory and with problems related to the growth of semigroups of matrices.