Vous êtes certainement familier des ondes stationnaires qui existent sur les instruments de musique à cordes. Vous savez que le musicien change la note jouée en déplaçant la position de sa main sur le manche de la guitare. Ce faisant, il ajuste la longueur de la corde, donc la longueur d'onde de la fondamentale qu'il excite. Cette vibration est ensuite amplifiée par la résonance de la caisse de la guitare.

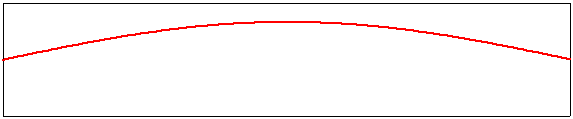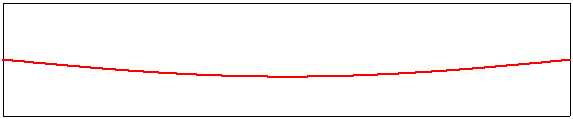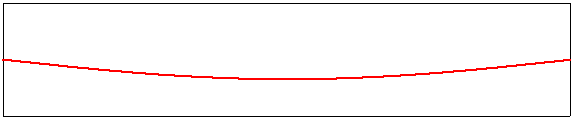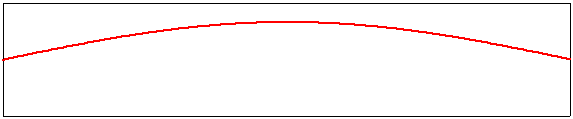
Sur une corde de longueur donnée L, fixée à ses deux extrémités, la fondamentale a une longueur d'onde lam_1=2L. La fréquence f1 de cette fondamentale est simplement donnée par le rapport entre la vitesse v de propagation d'une onde sur la corde (à ne pas confondre avec la vitesse de propagation du son qui atteint finalement vos oreilles!), et la longueur d'onde : f1 = v / lam_1 = v / (2L). Voici à quoi ressemble une corde supportant une onde stationnaire fondamentale. Attention! la vitesse de battement a été considérablement ralentie pour vous permettre de voir ce qui se passe.

mode fondamental, m=1 lam_1 = 2L f1 = v / (2L)

Vous identifierez facilement sur cette image les deux noeuds fixes et le ventre de l'onde stationnaire, et vous vérifierez sans peine que la longueur d'onde de la fondamentale est le double de la longueur de la corde.

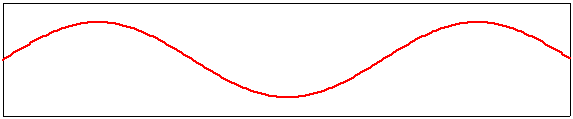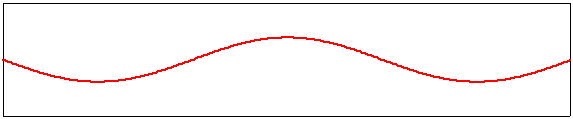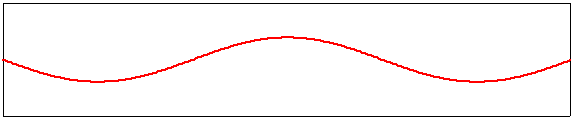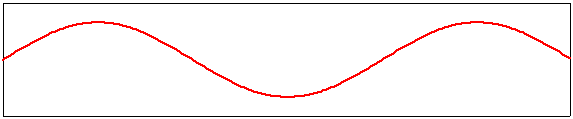
D'autres modes de vibration de la corde de longueur L sont possibles. Ces modes sont les harmoniques, dont les trois premières sont données ci-dessous.

deuxième harmonique, m=2 lam_2 = L f2 = 2.f1

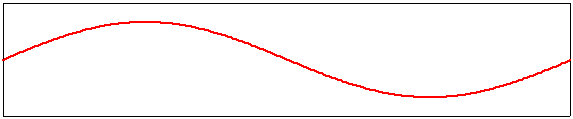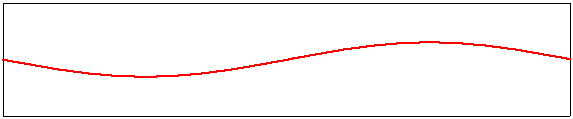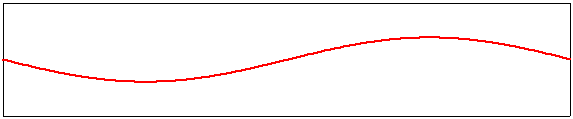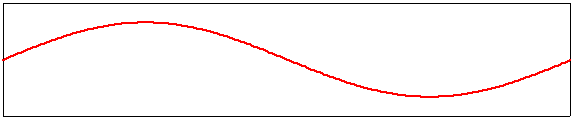troisième harmonique, m=3 lam_3 = 2L / 3 f3 = 3.f1

quatrième harmonique, m=4 lam_4 = L / 2 f4 = 4.f1

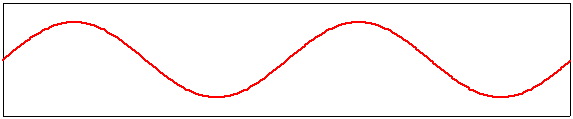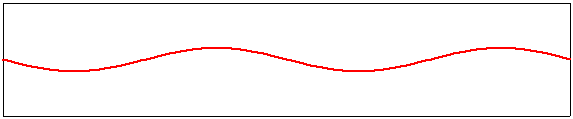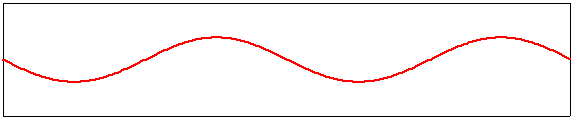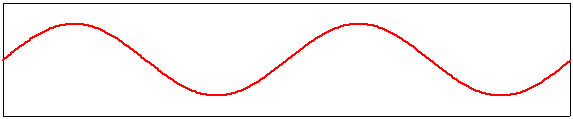Ces modes propres harmoniques sont des solutions stationnaires de l'équation d'onde qui respectent l'exigence d'avoir deux points fixes aux extrémités de la corde. Vous remarquerez que leur fréquence de vibration augmente proportionnellement à leur ordre m. Lorsque la corde est sollicitée par le musicien, ces harmoniques coexistent avec le mode fondamental; la hauteur du son est fixée par la fondamentale, mais le timbre perçu par l'oreille est essentiellement déterminé par la distribution des harmoniques existant sur la corde. Un aperçu d'une corde supportant plusieurs modes propres de vibration est donné ci-dessous. Ici, on a choisi une amplitude de 1 pour m=1, de 0,1 pour m=2, de -0,15 pour m=3, de 0,1 pour m=4 et de -0,05 pour m=5. Cette vibration spécifique n'est pas très probable, mais c'est bien une des solutions possibles de l'équation d'onde possédant deux points fixes aux extrémités de la corde.

Exemple de superposition d'un mode fondamental et des quatre harmoniques suivantes.

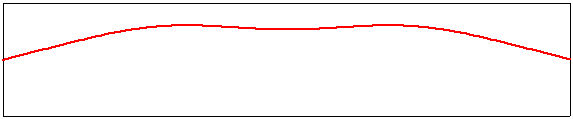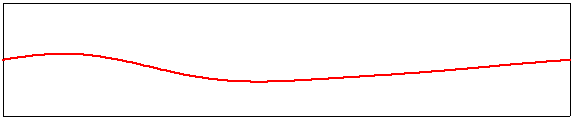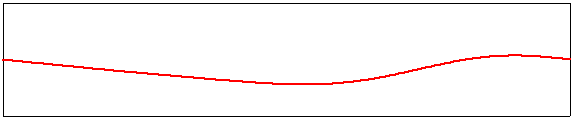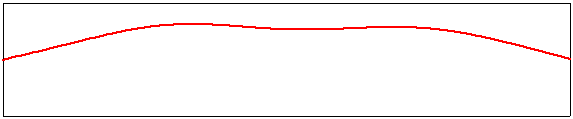Pour ajuster la fréquence, le musicien peut aussi jouer sur la vitesse v, ce dont il ne se prive d'ailleurs pas. La vitesse de propagation d'une onde mécanique sur une corde est donnée par la racine carrée du rapport entre la tension dans la corde et sa masse par unité de longueur. Vous savez que la guitare s'accorde en ajustant la tension des cordes; quant à la tessiture de la guitare, elle est élargie en utilisant 6 cordes de diamètre différent, donc de masse par unité de longueur différente.

Mais une fois la corde accordée et son diamètre fixé, le musicien n'a plus que la longueur de la corde comme paramètre variable (sans compter les multiples façons de faire vibrer la corde, et tous les petits trucs techniques maîtrisés par un bon musicien). Monter d'une octave correspond à un doublement de la fréquence fondamentale, donc à un raccourcissement par un facteur 2 de la longueur de la corde. Monter d'une quinte juste (de do à sol, par exemple) revient à multiplier la fréquence fondamentale par 3/2, donc à raccourcir la corde aux deux tiers de sa longueur initiale. La première harmonique d'un sol est donc égale à la seconde harmonique du do, et c'est cette coïncidence qui fait que cet intervalle est agréable à l'oreille.

Monter d'un demi-ton correspond à peu près à multiplier la fréquence fondamentale par un facteur égal à la racine douzième de 2 (il y a 12 demi-tons par octave). Pourquoi à peu près? Parce qu'il y a plusieurs façons d'accorder un instrument, selon les intervalles dont on veut privilégier la justesse - mais ceci est une histoire trop complexe pour cette petite page d'introduction. Simplement, vous pouvez réaliser qu'il y a un problème, puisque monter d'une quinte juste (7 demi-tons) revient à multiplier par 3/2=1,5 la fréquence, tandis qu'avec notre définition du demi-ton monter de 7 demi-tons revient à multiplier la fréquence par 2^(7/12)=1,498... Or, on devrait avoir la même chose. Pour obtenir un peu plus d'information sur ce sujet, vous pouvez par exemple consulter le chapitre 3 du petit livre très simple d'accès de Leon Harkleroad: The Math Behind the Music, Cambridge University Press: Cambridge, 2006, et les nombreuses références reprises à la fin du livre.

Page suivante