2 Un modèle très simple.
Des acteurs a1, a2,..., aN répartis sur la droite réelle
constatent la décroissance avec le temps de
la proportion de monnaie indigène (ou autochtone)
qu'ils détiennent. On note yi(t) la proportion détenue par ai
au temps t. Soit t0 le temps moyen d'échange de toute
la monnaie d'un acteur avec ses deux voisins, donc,
 |
|
yi(t+t0) = |
yi-1(t)+yi+1(t)
2
|
|
| (1) |
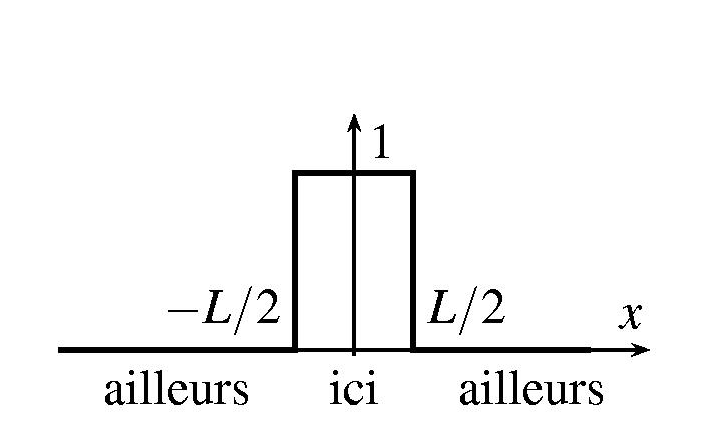
avec initialement yi(0)=1 sur un intervalle de longueur L et
yi(0)=0 ailleurs (il ne sagit que de la proportion de monnaie du
pays considéré, la quantité d'argent détenue par les gens
ne change pas
.
Exercice: qu'obtient-on si y(0)=1 pour une seule valeur de i?
|
On a aussi
|
yi(t+t0)-yi(t) = |
yi-1(t)-2yi(t)+yi+1(t)
2
|
|
|
ou encore
|
|
yi(t+t0)-yi(t)
t0
|
= |
d02
2t0
|
|
yi-1(t)-2yi(t)+yi+1(t)
d02
|
|
|
si d0 est la distance moyenne entre deux acteurs. Les quotients
ainsi mis en évidence sont proches de dérivées:
|
|
¶y(x,t)
¶t
|
= |
d02
2t0
|
|
¶2 y(x,t)
¶x2
|
|
| (2) |
Suggestion: résoudre (2) par transformée de Fourier ou
de Laplace (bilatérale).
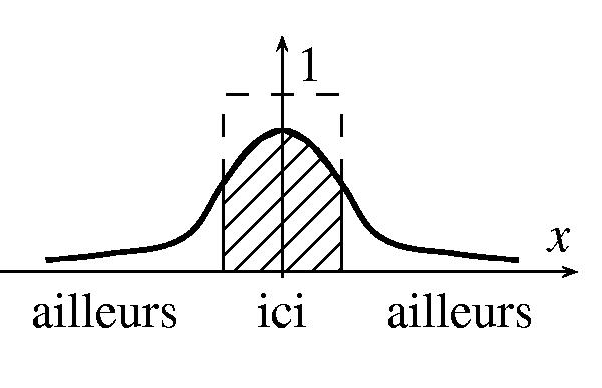 |
Au temps t > 0, la distribution uniforme confinée au pays
d'origine s'est affaisée et a quelque peu envahi les pays voisins.
La proportion encore disponible dans le pays d'origine (c'est la
valeur la plus facile à mesurer) est donnée par la partie
hachurée
|
Y(t) = |
1
L
|
|
ó
õ
|
L/2
-L/2
|
y(x,t) dx |
|
Voir ici une animation
|
| 
