Fragments d'argentologie. Traitement de l'eurotomanie.
INMA2375. Notes de projet intégré MAP 2002-2003.
|
voir § 6
|
Institut de Mathématique Pure et Appliquée, Université Catholique de Louvain, Chemin du Cyclotron,2, B-1348 Louvain-la-Neuve (Belgium) 010 47 3157 , magnus@anma.ucl.ac.be , http://www.math.ucl.ac.be/~magnus/
|
Ce fichier est http://www.math.ucl.ac.be/~magnus/eurodiff.htm
1 Présentation.
Depuis janvier 2002, nous pouvons suivre des pièces de monnaie à la trace. Comment décrire, et peut-être prévoir, le comportement dans le temps de la répartition des pièces de différentes origines?
1.1 Evolution de la concentration d'un milieu continu.
Il s'agit de déterminer dans quelle mesure l'argent se comporte comme une substance pâteuse s'affaisant lentement. Dans le modèle le plus simple (voir plus loin, en § 2), on décrit cette évolution en fonction d'un ou plusieurs paramètres à estimer.
1.2 Traitement de signal.
On essaye de se retrouver dans le fouillis d'irrégularités constatées à partir de mesures plus ou moins fiables, au § 3.
1.3 Etude d'un processus aléatoire.
Des probabilités de transfert devraient expliquer les résultats des observations, § 4.
1.4 Autres voies d'approche.
Vous trouverez peut-être de l'inspiration en voyant le phénomène sous l'angle de la cinétique chimique, ou de la physique des semi-conducteurs, physique du solide, ou de capillarité, d'osmose, etc.
2 Un modèle très simple.
Des acteurs a1, a2,..., aN répartis sur la droite réelle constatent la décroissance avec le temps de la proportion de monnaie indigène (ou autochtone) qu'ils détiennent. On note yi(t) la proportion détenue par ai au temps t. Soit t0 le temps moyen d'échange de toute la monnaie d'un acteur avec ses deux voisins, donc,
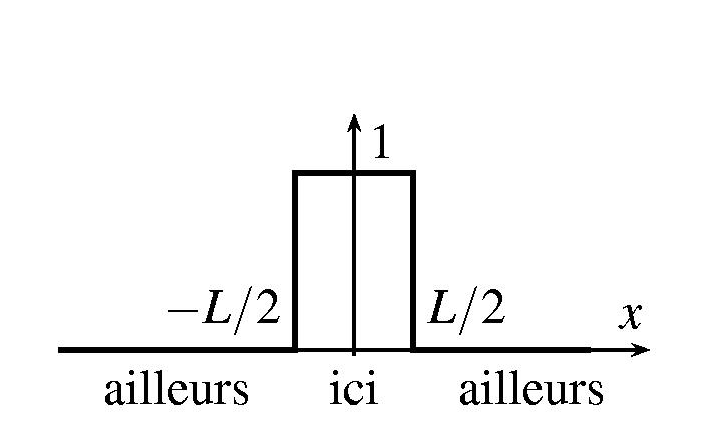 |
Exercice: qu'obtient-on si y(0)=1 pour une seule valeur de i? |
|
|
| (2) |
Suggestion: résoudre (2) par transformée de Fourier ou de Laplace (bilatérale).
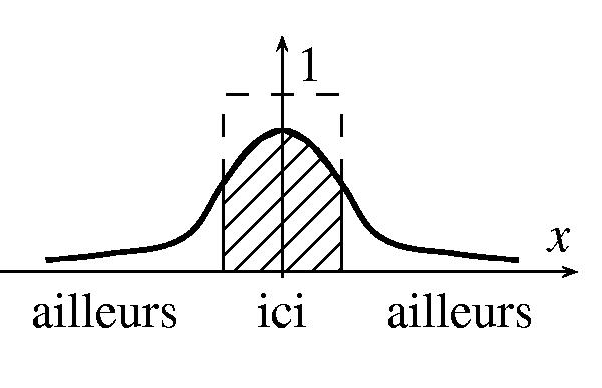 |
Au temps t > 0, la distribution uniforme confinée au pays
d'origine s'est affaisée et a quelque peu envahi les pays voisins.
La proportion encore disponible dans le pays d'origine (c'est la
valeur la plus facile à mesurer) est donnée par la partie
hachurée
Voir ici une animation |
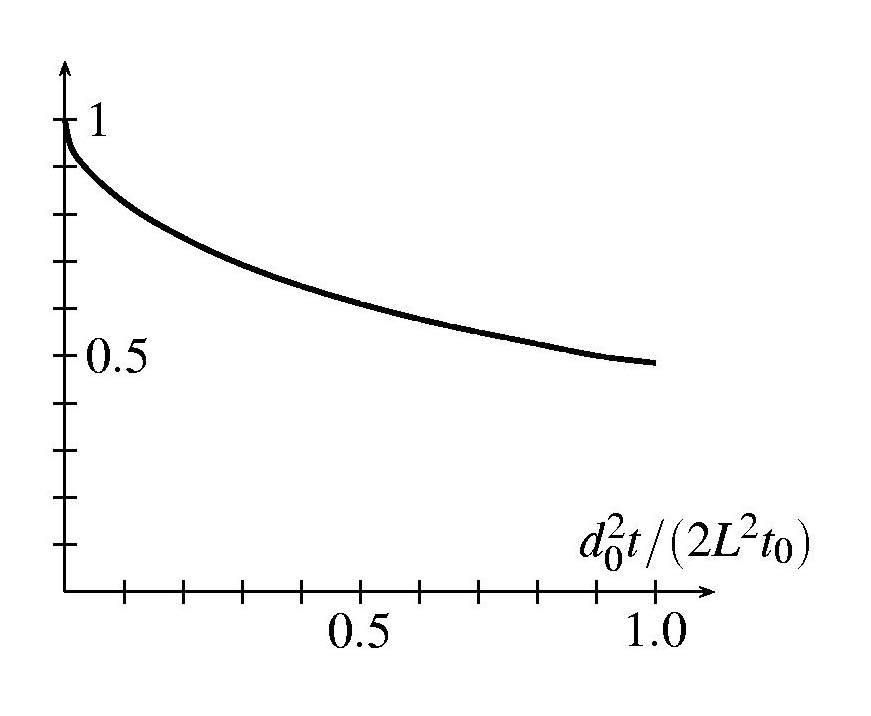 |
Cette moyenne nationale décroît avec t selon une fonction
universelle F de st, avec
Remarque: pourquoi passer au modèle analytique (2)?
La relation (1) est immédiatement calculable, mais
(2) montre l'importance de s. Amélioration: il
faudrait évidemment traiter le problème à deux
dimensions
Bon, avec d0 » 1 km (distance moyenne au supermarché ou à
la pompe la plus proche
|
Truckersfactor: (voir Wat is de 'truckersfactor'?) si on donne comme première source de diffusion les chauffeurs routiers internationaux, d0 peut être estimé non pas à un, mais à une centaine de kilomètres! On aurait alors d02/(2t0 L2) proche de 1 mois-1!
3 Traitement de signal, filtrage.
On voit que la théorie précède l'observation. Eh bien, observons. Une énorme documentation portant sur des mesures effectuées par des centaines de gens aux Pays-Bas et en Belgique (du nord...) est rassemblée à http://www.wiskgenoot.nl/eurodiffusie)
On y voit, parmi d'autres informations disponibles (voir leur section ``download'' ), la répartition des monnaies en Belgique et aux Pays-Bas en fonction du temps:
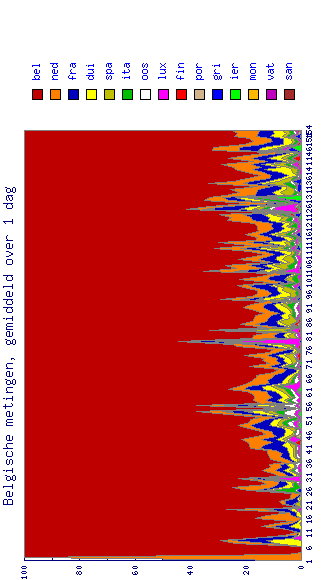
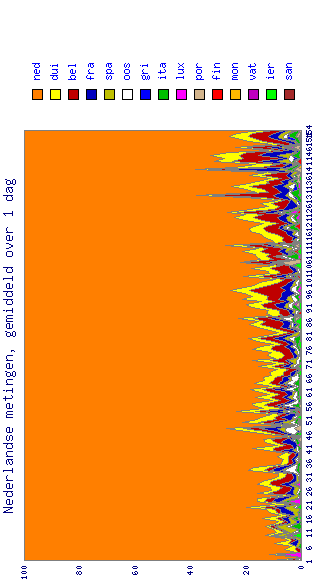
(Valeurs limitées au 3 juin 2002).
Ne retenons que la proportion nationale:
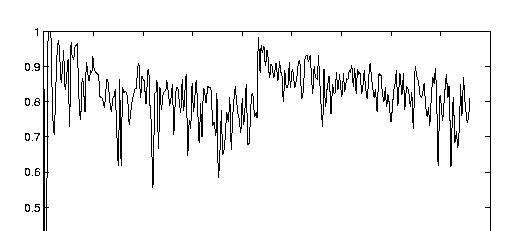
Que de bruit! Parfois dû au petit nombre d'informateurs (jours de congé,...), surtout en Belgique.
Extraction brute de s à partir de Y(t) » F(st): st » F-1(Y(t)):
% testpng.m: traitement de mesures 0 <= y <=1
clear;
%fnom=input('nom du fichier (entre apostrophes) ');
fnom='c:\lang\djgpp\bel3ju.d';
fid=fopen(fnom);
y1=fscanf(fid,'%f');
fnom='c:\lang\djgpp\ned3ju.d';
fid2=fopen(fnom);
y2=fscanf(fid2,'%f');
y=[y1' y2'];
plot(y);
print -dps testpng1.ps
% F -1 (y):
at=min( pi*(1./(y+0.0001)-1).^2,0.5);
plot(at);
print -dps testpng2.ps
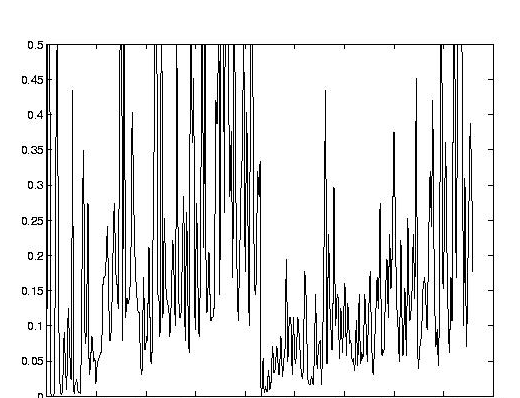
On a donc st » 0.25 en t=5 mois, d'où s = quelques centièmes de mois-1 pour la Belgique et les Pays-Bas.
Cas du Luxembourg. Voir eurlux.txt
4 Processus aléatoires.
| ...we should express the infinite smallness that surounds us, the imperceptible, the invisible, the agitation of atoms, the Brownian movements, all exciting hypotheses and all the domains explored by the high-powered microscope. (Marinetti, 1913 Manifesto) http://www.kmtspace.com/futurism.htm |
Problème à deux pays ou régions 'ici' et 'ailleurs'.
cf. http://www.wiskgenoot.nl/eurodiffusie/theorie/theorie.html) , http://www.wiskgenoot.nl/eurodiffusie/theorie/studiegroepmodel.html)
Soient p la probabilité qu'une pièce reste ici
après un mois (la prob. de sortie est donc 1-p), et q
la probabilité qu'une pièce
étrangère reste ailleurs. Alors, les quantités
présentes de pièces de m espèces seront
| (4) |
Que valent les p et q du Benelux, de la Flandre versus Wallonie, etc?
Nombreuses autres considérations dans
Linkname: Monte Carlo-simuloinnit / Monte Carlo simulations URL: http://beam.helsinki.fi/~knordlun/mc/
Linkname: Exercise X (bonus): The diffusion of euro coins URL: http://beam.helsinki.fi/~knordlun/mc/excX.ps
Pour un exemple beaucoup plus élaboré, voir
Linkname: Example 3. A complex system
URL: http://www.math.uu.se/~ikaj/courses/matlab/rcomplex.html
Linkname: gzipped tar-archive URL: http://www.math.uu.se/~ikaj/courses/matlab/stochsim_mfiles.tar.gz
5 Personnes à contacter.
Le projet de cette année est organisé par des membres de l'unité d'analyse numérique et de mathématiques appliquées: magnus@anma.ucl.ac.be , vdooren@csam.ucl.ac.be. Les autres responsables du projet intégré sont bastin@auto.ucl.ac.be , blondel@csam.ucl.ac.be , campion@auto.ucl.ac.be , wertz@auto.ucl.ac.be , wolsey@core.ucl.ac.be .
6 Plus sur la mystérieuse pièce italienne de 20c.
|
Il Simbolo von Umberto Boccioni. Il Simbolo è tratto da
"forme uniche nella continuità dello spazio".
Galleria d`Arte Moderna, Milano
(Les formes uniques de continuité dans l'espace)
http://www.geocities.com/eurocoin2003/revers/it/revit.html http://www.geocities.com/eurocoin2003/revers/it/hr0-2revit.jpg |
http://digilander.iol.it/giagia/formeuniche.htm
Linkname: italian futurism : boccioni, carra & de chirico
u. boccioni:unique forms of continuity in space - 1913
Umberto Boccioni 's simultaneity and dynamism searchs to capture a
sense of time that is implicit in being. Like Bergson's notion of
'duration' as the principle animating the passage through time rather
than the particular form at a given instant, his work observes the
lifelessness of a form arrested from motion in a single instant, and
creates forms that are condensed records of their own becoming...
Unique Forms of Continuity in Space of 1913 anticipate the tools and
concepts of scientific visualization, especially isosurfaces. (Marcos
Novak)
http://www.kmtspace.com/futurism.htm
Mais non, voyons.
7 Sponsors.
