The "One-Ninth" Constant

We are concerned here with rational approximation of exp(-x) on the half-line [0,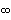). Let 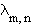denote the error of best uniform approximation:

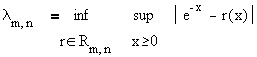
where

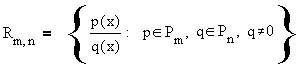
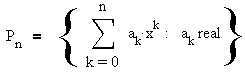
There are two cases of special interest, when m=0 and m=n, since clearly

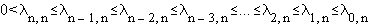
Many researchers [1,2,10] have studied these constants 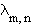, referred to as Chebyshev constants in [2]. We mention the work of only a few. Schönhage [11] proved that

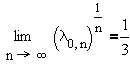
which led several people to conjecture that

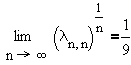
Numerical evidence uncovered by Schönhage [12] and Trefethen & Gutknecht [13] suggested that the conjecture is false. Carpenter, Ruttan and Varga [14] calculated the Chebyshev constants to an accuracy of 200 digits up to n = 30 and carefully obtained

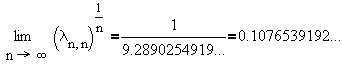
although a proof that the limit even existed was still to be found.

Building on Opitz & Scherer [15] and Magnus [16], Gonchar & Rakhmanov [2,3] proved that the limit exists and that it equals

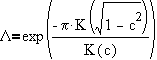
where K is the complete elliptic integral of the first kind

and the constant c is defined as follows. Let E be the complete elliptic integral of the second kind

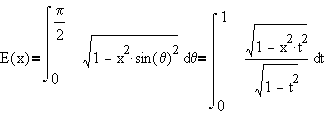
(One's first encounter with K and E is often with regard to computing the period of a physical pendulum and finding the arclength of an ellipse.) The constant c is defined simply as the unique solution, 0 < c < 1, of the equation

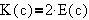
The appearance of elliptic integrals here reminds one of work done over one hundred years before. In 1877, Zolotarev determined a number of exact solutions to approximation problems using elliptic functions [1] in research which was far ahead of its time. See Bernstein's constant for more details.

Gonchar and Rakhmanov's exact disproof of the "one-ninth" conjecture utilized ideas from complex potential theory, which seems far removed from the rational approximation of exp(-x)! They also obtained a number theoretic characterization of the "one-ninth" constant . If

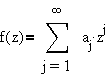
where

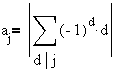
then f is complex-analytic in the open unit disc. The unique positive root of the equation

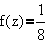
is the constant 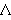. Another way of writing a_j is as follows [5]. If

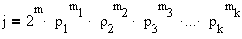
is the prime factorization of the integer j, where each p_i is an odd prime, m ≥ 0 and m_i ≥ 1 , then

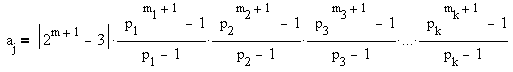
Carpenter [2] computed 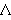to 101 digits using this equation.

Here is another expression due to Magnus [16]. The one-ninth constant 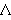is the unique solution, with 0 < x < 1, of the equation

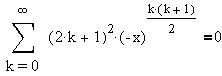
which turns out to have been studied one hundred years earlier by Halphen [4]. Halphen was interested in theta functions and computed 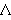to six digits, clearly unaware that this constant would become prominent a century later! Varga [2] has suggested that 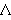be renamed the Halphen constant. So many researchers have contributed to the solution of this approximation problem, however, that retaining the amusingly inaccurate "one-ninth" designation might be simplest.

Relevant Mathcad files will be included as time permits. Plouffe gave accurate approximations of 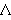and 1/ 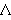in the Inverse Symbolic Calculator web pages.

Postscript

The constant c=0.9089085575... defining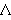

arises in a completely unrelated field: the study of Euler elasticae [6-8].

A quotient of elliptic functions, similar to that above, occurs in our essay on Grötzsch ring constants.

References

P. P. Petrushev and V. A. Popov, Rational Approximation of Real Functions, Cambridge Univ. Press, 1987; MR 89i:41022.
R. S. Varga, Scientific Computation on Mathematical Problems and Conjectures, SIAM, 1990; MR 92b:65012.
A. A. Gonchar and E. A. Rakhmanov, Equilibrium distributions and degree of rational approximation of analytic functions, Math. USSR Sbornik 62 (1989) 305-348; MR 89h:30054.
G.-H. Halphen, Traité des fonctions elliptiques et de leurs applications, v. 1, Gauthier-Villars, 1886, p. 287 (Cornell Digital Library).
A. A. Gonchar, Rational approximations of analytic functions, Amer. Math. Soc. Transl. Ser. 2, 147 (1990) 25-34; MR 89e:30066.
D. A. Singer, Curves whose curvature depends on distance from the origin, Amer. Math. Monthly 106 (1999) 835-841; MR 2000j:53005.
T. A. Ivey and D. A. Singer, Knot types, homotopies and stability of closed elastic rods, Proc. London Math. Soc. 79 (1999) 429-450; MR 2000g:58015.
C. Truesdell, The influence of elasticity on analysis: The classic heritage, Bull. Amer. Math. Soc. 9 (1983) 293-310; MR 85f:01004.
R. S. Varga, Topics in Polynomial and Rational Interpolation and Approximation, Les Presses de l'Université de Montréal, 1982; MR 83h:30041.
W. J. Cody, G. Meinardus and R. S. Varga, Chebyshev rational approximations to e^-x in [0,+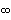) and applications to heat-conduction problems, J. Approx. Theory 2 (1969) 50-65; MR 39 #6536.
A. Schönhage, Zur rationalen Approximierbarkeit von e^-x über [0,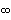), J. Approx. Theory 7 (1973) 395-398; MR 49 #3391.
A. Schönhage, Rational approximation to e^-x and related L²-problems, SIAM J. Numer. Anal. 19 (1982) 1067-1080; MR 83k:41016.
L. N. Trefethen and M. H. Gutknecht, The Carathéodory-Fejér method for real rational approximation, SIAM J. Numer. Anal. 20 (1983) 420-436; MR 85g:41024.
A. J. Carpenter, A. Ruttan, and R. S. Varga, Extended numerical computations on the "1/9" conjecture in rational approximation theory, Rational Approximation and Interpolation, Lecture Notes in Math. 1105, Springer-Verlag, 1984, pp. 383-411.
H.-U. Opitz and K. Scherer, On the rational approximation of e^-x on [0,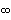), Constr. Approx. 1 (1985) 195-216; MR 88f:41027.
A. P. Magnus, On the use of the Carathéodory-Fejér method for investigating "1/9" and similar constants, Nonlinear Numerical Methods and Rational Approximation, Reidel, 1988, pp. 105-132, MR 90j:65035.
A. P. Magnus, Asymptotics and super asymptotics for best rational approximation error norms to the exponential function (the "1/9" problem) by the Carathéodory-Fejér method, Nonlinear Numerical Methods and Rational Approximation II, Kluwer, 1994, pp. 173-185; preprint; MR 96b:41023.
A. P. Magnus and J. Meinguet, The elliptic functions and integrals of the "1/9" problem, Numer. Algor. 24 (2000) 117-139 ; preprint.

Return to the Favorite Mathematical Constants main essay.