About¶
News¶
- I just submitted a paper to the 62nd Conference on Decision and Control (2023), which will be held in Singapore, December 2023 <https://cdc2023.ieeecss.org/>.
- Along our toolbox to test the local identifiability of a network, we have added a code to check the potential equivalence of decoupled and local identifiability. [code]
Research: Network identifiability¶
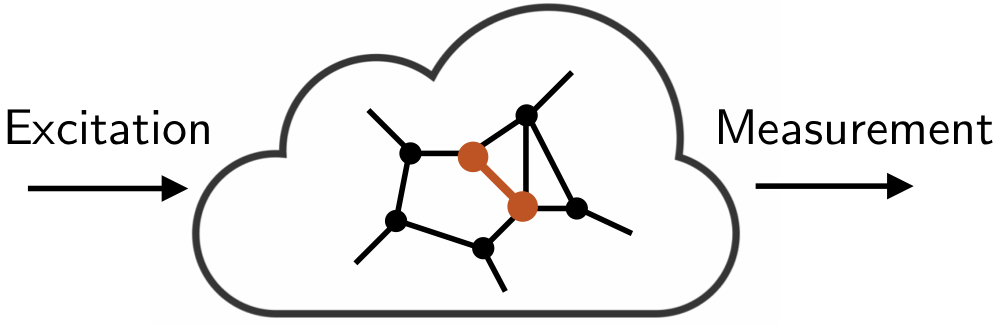
Networked systems consist of the interconnection of several dynamical systems. Applications include for example power networks (smart grids), biochemical networks, neurobiology, transportation networks, multi- agent robotics, or social networks. The network structure, i.e. the graph of the interconnections, has a major impact on the behavior of these systems, but also on our ability to analyze their local dynamics from global observations.
In my thesis we propose a new approach to network identification: we determine the conditions under which one can recover the local dynamics from the global input-output behavior of the networked system and the network structure. Graph-theoretical problems play an important role in our work.
We focus more particularly on LTI networked systems where a subset of the nodes is measured and a subset of the nodes is subject to external excitation (these subsets may intersect and do not necessary cover the whole network). We suppose that the input-output behavior of the system has been identified and that the network structure is known. We want to determine the conditions under which all or specific local transfer functions can then be re-identified.
Here are a poster and a vulgarized summary of my research.