FSAC 1430 Physique T4 : électricité et magnétisme
Semaine 2 : Électrostatique (seconde partie)

APE (apprentissage par exercices)
Chaque étudiant doit préparer, en groupe ou seul, une solution
pour les exercices 1, 4, 5 et 8 de la liste ci-dessous. Lors de la seconde séance de
tutorat, chacun doit pouvoir présenter cette solution et pouvoir répondre aux
questions posées par le tuteur en utilisant uniquement cette solution et
son document de synthèse personnel (4 pages maximum).
Liste
1. Une charge Q est uniformément répartie sur une surface
hémisphérique de rayon a .
Trouvez les champs
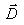 et
et 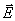 ,
au centre de courbure P de cette surface.
,
au centre de courbure P de cette surface.
Calculez aussi le potentiel V au point P en
supposant que le potentiel est nul "à l'infini".
Pour réaliser la situation décrite dans l'énoncé, faut-il
utiliser un hémisphère isolant ou conducteur ?
2. Young & Freedman, éd. 10, page 702, exercice 22-84 (ou éd. 11,
page 835, exercice 21-102) +
Que vaut le champ 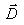 sur l'axe ?
Que peut-on dire des champs
sur l'axe ?
Que peut-on dire des champs 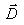 et
et
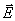 à grande distance, y compris en dehors
de l'axe ? L'anneau est-il conducteur ou isolant ?
à grande distance, y compris en dehors
de l'axe ? L'anneau est-il conducteur ou isolant ?
3. Young & Freedman, éd. 10, page 726, exercice 23-18 (ou éd. 11,
page 864, exercice 22-26) +
Calculez aussi les valeurs de 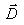 .
.
4. Une charge de 1.5 mC est placée à une hauteur
de 4 m au-dessus du sol, considéré comme un plan conducteur de potentiel V nul.
Que valent les champs 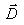 et
et
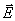 en chaque point (situé juste au-dessus) du
sol ?
en chaque point (situé juste au-dessus) du
sol ?
Que vaut la densité de charge électrique à la
surface du sol ?
Indication : les figures 24.17b, page 747 et 24.18, page 748 de Young &
Freedman, éd. 10 ( ou les figures 23.23b, page 891 et 23.24, page 892 de Young &
Freedman, éd. 11) peuvent vous inspirer une méthode de calcul.
5. On considère deux droites parallèles très longues, l'une
portant une densité de charge l (en C/m) et l'autre
une densité de charge -l. Soit 2d la distance
entre ces deux droites.
Montrez que l'on peut définir le potentiel de telle façon qu'il soit nul à
grande distance des droites.
Montrez que les équipotentielles sont des surfaces cylindriques.
Quels sont les rayons de deux équipotentielles de valeur VA et
-VA ? Quelle est la distance 2 h entre les centres de ces équipotentielles ?
En vous aidant des résultats ci-dessus, calculez la capacité d'un condensateur
formé de deux cylindres conducteurs de rayon R et de distance (entre axes) 2 h.
6. Young & Freedman, éd. 10, page 794, exercice 25-29 (ou éd. 11,
page 937, exercice 24-41) +
Quel est le volume minimum d'un tel condensateur (en négligeant l'épaisseur
des électrodes) ?
Que valent les champs 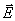 et
et
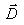 dans ce condensateur ?
dans ce condensateur ?
Calculez l'énergie du condensateur de trois façons différentes,
en utilisant
- la densité d'énergie exprimée en fonction des champs,
- l'expression de l'énergie d'un condensateur en terme de grandeurs de type circuit,
- une expression de l'énergie en terme de la répartition du potentiel V et
de la densité de charge r.
Pourquoi doit-on faire intervenir un facteur 1/2 dans ce dernier cas, alors que, en semaine 1,
il n'intervenait pas dans l'exercice 3 de l'APE ?
7. Young & Freedman, éd. 10, page 794, exercice 25-33 (ou éd. 11,
page 937, exercice 24-45) +
Que valent les champs 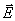 et
et
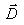 dans ce condensateur ?
dans ce condensateur ?
Recalculez l'énergie du condensateur en utilisant deux méthodes autres que
celle que vous avez utilisée pour répondre à la question
précédente, et comparez le résultat
à l'énergie figurant dans les données de l'exercice.
Comparez l'augmentation d'énergie du condensateur à l'énergie fournie par
l'alimentation électrique pendant l'introduction de la plaque. Expliquez d'où peut
provenir une éventuelle différence.
8. Young & Freedman, éd. 10, page 798, exercice 25-62 (ou éd. 11,
page 941, exercice 24-78) +
Calculez la répartition du champ 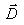 dans ce dispositif.
dans ce dispositif.
Calculez l'énergie du condensateur de trois façons différentes,
en utilisant
- la densité d'énergie exprimée en fonction des champs,
- l'expression de l'énergie d'un condensateur en terme de grandeurs de type circuit,
- une expression de l'énergie en terme de la répartition du potentiel V et
de la densité de charge r.
Pourquoi doit-on faire intervenir un facteur 1/2 dans ce dernier cas, alors que, en semaine 1,
il n'intervenait pas dans l'exercice 3 de l'APE ?

Retour au menu de la semaine 2
Dernière mise à jour le 23-09-2004
et
en chaque point (situé juste au-dessus) du
sol ?