FSAC 1430 Physique T4 : électricité et magnétisme
Semaine 10 : Équations de Maxwell et synthèse

Exercices relatifs aux équations de Maxwell
1. Young & Freedman, ed. 10, p. 935, ex. 29-36 (or ed. 11, p. 1141, ex. 29-36) + ...
Suppose that the parallel plates in figure S10-11 have an area of 3.00 cm2 and are separated by a 2.50-mm-thick sheet of dielectric that completely fills the volume between the plates.
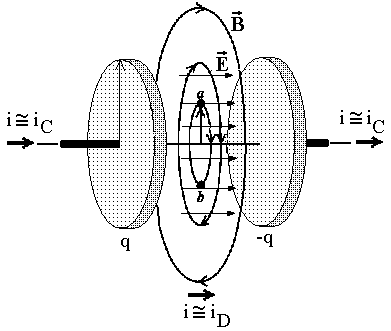
Figure S10-11
The dielectric has dielectric constant 4.70. (You can ignore fringing effects.) At a certain instant, the potential difference between the plates is 120 V and the current i equals 6.00 mA. At this instant, what is
- the charge q on each plate;
- the rate of change of charge on the plates;
- the current density J , the field D in the dielectric and its derivative ¶
D / ¶
t;
- the surface integral of ¶
D / ¶
t on a plane perpendicular to the axis;
- the displacement current in the dielectric?
2. Young & Freedman, ed. 10, p. 935, ex. 29-37 (or ed. 11, p. 1141, ex. 29-35) + ...
A parallel-plate air-filled capacitor is being charged as in figure S10-11. The circular plates have radius 4.00 cm, and at a particular instant the current in the wires is 0.280 A.
- What is the displacement current density JD in the air space between the plate?
- What is the rate at which the field D and the electric field E between the plates are changing?
- What is the induced magnetic field between the plates at a distance of 2.00 cm from the axis?
- at 1.00 cm from the axis?
3. Young & Freedman, ed. 10, p. 936, ex. 29-38 (or ed. 11, p. 1141, ex. 29-38)
A long, straight, copper wire with a circular cross-sectional area of 2.1 mm2 carries a current of 16 A. The resistivity of the material is 2.0 x 10-8 W.m.
- What is the uniform electric field in the material?
- If the current is changing at the rate of 4000 A/s, at what rate is the electric field in the material changing?
- What is the displacement current density in the material in part (b)? Hint: Since K for copper is very close to 1, use eo = eo .
- If the current is changing as in part (b), what is the magnitude of the magnetic field 6.0 cm from the center of the wire? Note that both the conduction current and the displacement current should be included in the calculation of B. Is the contribution from the displacement current significant?
4. Young & Freedman, ed. 10, p. 936, ex. 29-39 (or ed. 11, p. 1141, ex. 29-37) + ...
At Fig. S10-11, the capacitor plates have area 5.00 cm2 and separation 2.00 mm. The plates are in vacuum. The charging current i has a constant value of 1.80 mA. At t = 0, the charge on the plates is zero.
- Calculate the charge on the plates, the fields D and E between the plates, and the potential difference between the plates when t = 0.500 ms.
- Calculate dD/dt , the time rate of change of the electric displacement field between the plates. Does dD/dt varies in time?
- Calculate the displacement current density jD between the plates, and from this the total displacement current iD . Dow do iC in the conductors and iD in the dielectric compare?
Autres exercices de synthèse
5. Young & Freedman, ed. 10, p. 994, ex. 31-46 (or ed. 11, p. 1177, ex. 30-50) + ...
A small solid conductor with radius a is supported by insulating,
nonmagnetic disks on the axis of a thin-walled tube with inner radius b.
The inner and outer conductors carry equal currents i in opposite
directions.
- Use Ampere's law to find the magnetic fields H and B at
any point in the volume between the conductors.
- Write the expression for the flux
dFB through a narrow strip of
length l parallel to the axis, of width dr, at a distance r from the axis
of the cable and lying in a plane containing the axis.
- Integrate your expression from part (b) over the distance between the
two conductors to find the total flux produced by a current i in the
circuit.
- Show that the inductance of a length l of the cable is
(S10-30) 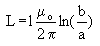
- Use equation
(S10-31) 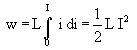
to calculate the energy stored in the magnetic field for a length l of the
cable.
- What is the analytic expression of the energy density
(S10-32) 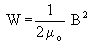
stored in the magnetic field. Then, integrating over the whole space,
calculate the energy stored and compare with answer (e).
6. Young & Freedman, ed. 10, p. 994, ex. 31-49 (or ed. 11, p. 1177, ex. 31-53) + ...
Uniform electric and magnetic fields E and B occupy the
same region of free space.
- If E = 650 V/m, what are B and H if the energy
densities in the electric and magnetic fields are equal?
- Which is the ratio between E and H? What is the physical dimension of
this ratio? Hint: it's a familiar unity of circuit theory.

Retour au menu de la semaine 10
Dernière mise à jour le 10-10-2004