Enoncé du projet.

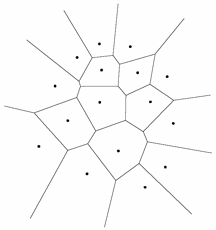
Diagramme de Voronoï

Soit un ensemble V = {v₁,...,v_N}, N ³ 3 de points du plan euclidien E². Si d(v_i,v_j) désigne la distance entre les points v_i et v_j, la région V(i) = {xÎE² | d(x,v_i) £ d(x,v_j), j=1,...,N} qui est le lieu des points plus près de v_i que tout autre point de V est appelée le polygone de Voronoï associé au point v_i.

La structuration des polygones de Voronoï est analogue à celle d’un processus d'expansion cellulaire. Supposons que chaque point de V soit le noyau d'une cellule. La cellule se propage dans toutes les directions à vitesse uniforme. L'expansion s'arrête quand le bord en expansion d'une cellule rencontre le bord d'une autre cellule. Le processus d'expansion cellulaire s'arrête quand les cellules couvrent le plan entier de polygones convexes, ce sont les polygones de Voronoï. 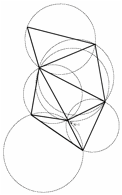Eventuellement, certaines cellules dont le noyau est situé sur H(V), le polygone convexe entourant V, voient leur expansion continuer indéfiniment. La Figure 1 montre un exemple de diagramme de Voronoï.

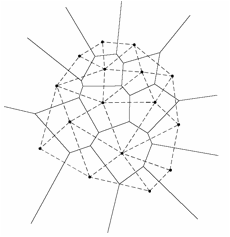
Figure 1 : A gauche, le diagramme de Voronoï. A droite, la triangulation de Delaunay

Triangulation de Delaunay

Regardons maintenant de plus près ce processus. Puisque toutes les cellules croissent à la même vitesse, le premier point de contact entre cellules se situe au point milieu de la droite reliant leurs noyaux. De la même façon, chaque point de contact se situera sur la bissectrice du segment reliant les deux noyaux. Cette bissectrice continue jusqu'à ce qu'elle rencontre une troisième cellule. Le point de rencontre est appelé point du Voronoï et la tranche de bissectrice arête de Voronoï. Deux cellules partageant une arête commune sont appelées voisins du Voronoi. La construction DT(V) qui consiste à rejoindre les noyaux des polygones voisins est appelée tessellation (ou triangulation) de Delaunay. Les points du Voronoï seront évidemment les centres des cercles circonscrits aux triangles. La triangulation de Delaunay et le diagramme de Voronoï sont deux constructions duales.

Algorithme de Bowyer et Watson

La triangulation de Delaunay possède certaines propriétés intéressantes. Nous en citerons une qui va nous servir pour la création d'un triangulateur automatique de Delaunay. Soit un ensemble de points V = {v₁,...,v_N}, Dv_iv_jv_k est un triangle de Delaunay de DT(V) si et seulement si son cercle circonscrit ne contient aucun autre point que v_i, v_j et v_k. C'est le théorème du cercle.

Notons qu’il existe de nombreux algorithmes permettant de trianguler un nuage de points sans passer par la génération du diagramme de Voronoï.

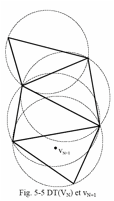
L'algorithme de Bowyer est un algorithme itératif. Il utilise le théorème du cercle. Considérons la triangulation de Delaunay DT(V_N) avec VN = {v₁,...,v_N}. Soit un point v_N+1 Î H(VN) (Figure 2). L'algorithme suivant permet de générer la triangulation de Delaunay DT(V_N+1) avec V_N+1 = { v₁,...,v_N, v_N+1 }.

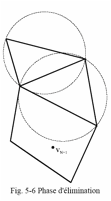
· On commence par éliminer tous les triangles de DT(V_N) dont le cercle circonscrit contient v_N+1, et cela en accord avec le théorème du cercle. Il est possible de démontrer que le polygone E(V_N, v_N+1) construit à partir des triangles éliminés est convexe et d'un seul tenant (Figure 2).

· On reconstruit la triangulation en reliant le point v_N+1 aux points de H(E). On obtient ainsi une nouvelle triangulation de Delaunay (Figure 2).

Figure 2 : Algorithme de Bowyer et Watson.

Notez que vous avez le choix dans l’algorithme pour la génération de la triangulation. Vous pouvez, outre l’algorithme de Bowyer et Watson, utiliser l’algorithme de Lawson ou la technique « divide and conquer » (diviser pour régner en français).

Cahier des charges

Reconstruire un objet à partir de données partielles est un problème important et ayant de nombreuses applications dans de nombreux domaines. En médecine par exemple, on cherche à reconstruire des modèles tri-dimensionnels des organes à partir de coupes scanner ; en géologie, la structure du sous-sol à partir de mesures sismiques, en ingénierie, un modèle CAO à partir de points mesurés sur une maquette.

La triangulation de Delaunay et le diagramme de Voronoï définissent une technique permettant de reconstruire une surface 2D (ou un volume si on travaille en 3D), si l'on dispose uniquement de points sur cette surface (ou sur ce volume).

Le but de ce projet est de construire une triangulation de Delaunay à partir d’une liste de données. Ces données sont fournies sous la forme d’un fichier organisé de la façon suivante :

X Y VAL

X Y VAL

…

X Y VAL

Le champ VAL du fichier est variable en fonction du type de champs à représenter :

· Une seule valeur réelle pour les champs scalaires ;

· Deux valeurs pour les deux composantes v_x et v_y d’un vecteur v ;

· Trois valeurs pour les trois composantes s_x, s_y et s_xy indépendantes d’un tenseur symétrique d’ordre 2 s.

Les résultats du programme à développer se présenteront sous la forme d’un fichier de sortie dont le format est défini dans la section 9.2.1 de la documentation de gmsh (http://www.geuz.org/gmsh/doc/texinfo/gmsh-full.html). On utilisera des triangles scalaires comme objets de sortie (voir la doc de gmsh ou l’exemple fourni en annexe).

Le résultat se présentera sous la forme d’un exécutable qui devra pouvoir être utilisé de la façon suivante :

programme [options] fichier.in fichier.out.

Le fichier.in se présentera sous la forme définie plus haut et le fichier.out devra être lisible par gmsh. Les [options] du programme sont facultatives sauf une, l’option ‑help. Quand l’option ‑help est activée, le programme doit écrire dans la sortie standard std::cout (ou stdout en langage C) une note explicative sur l’utilisation de celui-ci.

Deux déliverables devront être fournis dans le cadre de ce projet

· Une archive compressée (zip, rar ou tar.gz) contenant le code source ainsi qu’un fichier README dans lequel se trouveront les instructions pour la compilation et l’installation du programme. L’utilisation d’un makefile, de autoconf, la génération d’une manpage seront considérées avec la plus grande bienveillance par vos correcteurs.

· Un rapport concis (au maximum 7 pages A4 en Times 12) ou seront expliquées clairement vos choix de design tant au point de vue des structures de données que des algorithmes.

L’évaluation portera sur

· La facilité d’installation, de compilation ainsi que la qualité de la documentation (option –help ou man page). Si un programme ne compile pas, notre indulgence sera minime.

· La justesse du programme pour les exemples fournis par nos soins ;

· La robustesse du programme pour une série d’autres exemples. On veillera en outre à ce que la mémoire allouée soit bien libérée en vue d’éviter les fuites de mémoire (memory leaks). Dans l’environnement linux, il existe un logiciel pour détecter des fuites de mémoire automatiquement : « valgrind » ;

· L’efficacité du programme. Il serait judicieux de tester votre programme en utilisant au moins 10000, voire 100000 données. Si N est le nombre de points, un bon algorithme devrait avoir une complexité (temps d’exécution) de type N log(N). Un mauvais algorithme aura une complexité de N² ;

· La qualité du design ainsi que la qualité de l’implémentation. Trois classes devront obligatoirement être définies (d’autres classes pourront être définies en outre de celles là). Une classe pour les points, une classe pour les triangles et une classe pour les données. La classe « donnée » sera une classe virtuelle pure dont devront dériver des classes de donnée scalaire, vectorielle et tensorielle. Notez que vous allez être amenés à manipuler des conteneurs (listes, tableaux) de taille variable (le nombre de triangles augmente et certains triangles seront éliminés de la liste au cours de l’algorithme). L’utilisation de la Standard Template Library (STL, www.sgi.com/tech/stl) pourrait vous faciliter grandement la tâche.

Modalités

Le développement du programme se fera obligatoirement dans l’environnement LINUX. Pour ceux qui utiliseraient leur ordinateur personnel sous Windows, vous avez la possibilité d’installer un environnement de type LINUX (gratuit) en téléchargeant l’environnement cygwin (www.cygwin.com). Si vous deviez installer cygwin, installez l’ensemble des composants, y compris les outils de développement. Il existe une version minimale de cygwin sur http://www.mingw.org/ que nous n’avons pas vraiment testée mais qui jouit d’une bonne réputation. Il n’est évidemment pas interdit de développer votre code en utilisant autre chose mais il faut savoir que certains logiciels commerciaux bien connus ne fournissent pas un compilateur C++ qui respecte scrupuleusement la norme ANSI. Votre programme pourrait donc très bien compiler sur votre plateforme mais PAS sous LINUX.

Le logiciel gmsh est téléchargeable en version exécutable pour la plupart des plateformes standard (www.geuz.org/gmsh).

Exemple

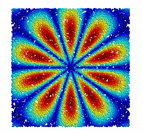
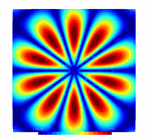
Voici un exemple simple qui montre le type de résultats attendus (les données sont disponibles sur le site Web du cours). Nous avons généré à l’aide de MATLAB trois fichiers Exemple1.in, Exemple2.in et Exemple3.in qui contiennent respectivement 200, 2000 et 20000 points entre dans les intervalles XÎ[–2p et 2p] et YÎ[–2p et 2p]. Les points sont choisis au hasard (fonction rand) et, en chaque point X Y (r, q), on a calculé la fonction v(r, q)=J1(r)sin(5q). Les résultats sont présentés dans les Figures 3,4 et 5.

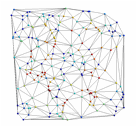
Figure 3 : Résultats de la triangulation pour l’exemple Exemple1.in avec 200 points.

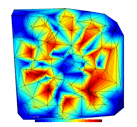
Figure 4 : Résultats de la triangulation pour l’exemple Exemple2.in avec 2000 points.

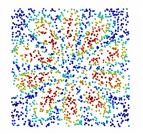
Figure 5 : Résultats de la triangulation pour l’exemple Exemple3.in avec 20000 points.

· Notez que, pour les 20000 points, l’algorithme utilisé par nos soins a nécessité beaucoup moins d’une seconde pour effectuer son travail (juste pour vous énerver un peu).

Bon travail.