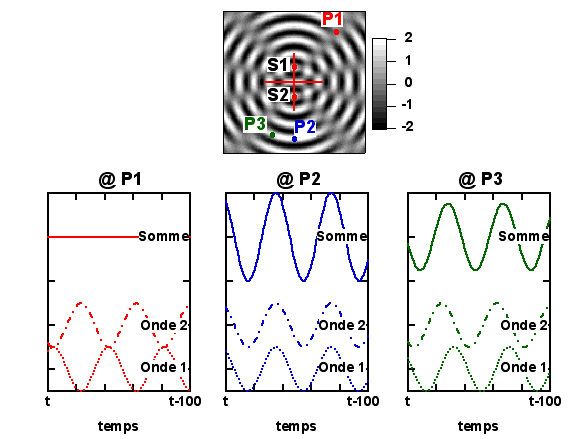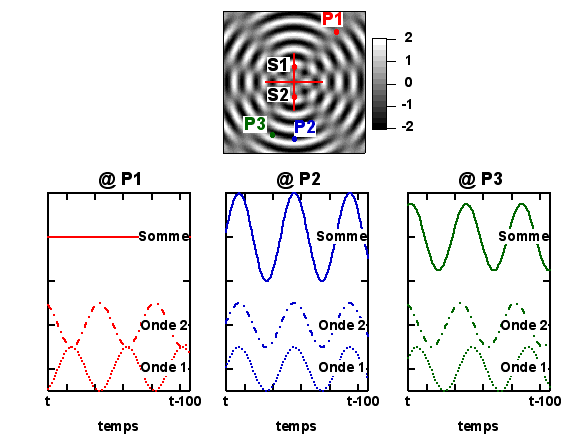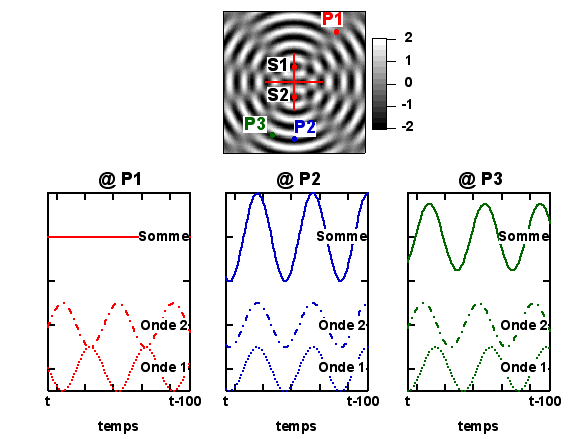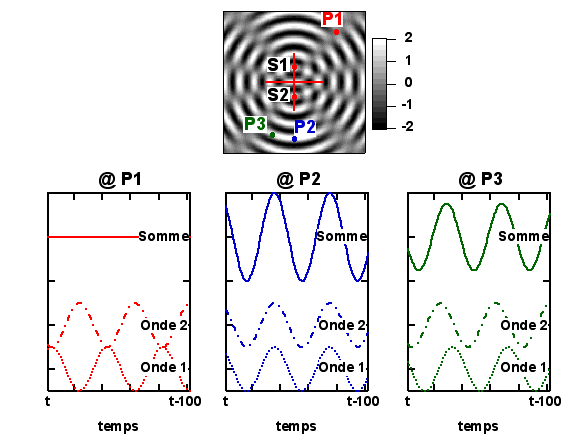
Continuons d'examiner le cas très simple de deux sources ponctuelles cohérentes, de même amplitude et de même polarisation, en négligeant toujours l'atténuation de leur amplitude avec la distance, et en travaillant toujours dans l'hypothèse du principe de superposition. Regardons la situation à différents points Pi de l'espace.

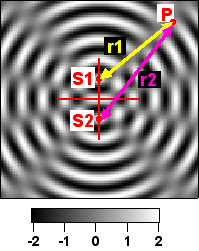
L'onde émise en S1 prend moins de temps à atteindre le point rouge (P1) que l'onde émise en S2. Le retard de l'une par rapport à l'autre est tel que les maxima de l'une correspondent aux minima de l'autre, et la résultante est nulle (figure de gauche, en bas) : l'interférence est destructive. En P2 par contre, le retard de la première onde par rapport à la seconde est tel que les maxima (et les minima) des deux ondes coïncident. Les ondes interfèrent de manière constructive, et l'amplitude de l'onde résultante est double de celle de chacune des ondes primaires. Enfin, en P3, la situation est intermédiaire.

Passons à une description mathématique de ces interférences. Nous allons écrire le champ total en un point P quelconque de l'espace. Pour fixer les idées, nous considérerons que les ondes primaires sont des ondes sphériques sinusoïdales polarisées linéairement dans la direction 1z.

Le champ créé en P par la première onde est de la forme , où r1 est la distance entre la première source et le point P, et est le nombre d'onde. De la même manière, le champ créé en P par la seconde onde est de la forme , où r2 est la distance entre la seconde source et le point P, et est un terme prenant en compte un éventuel déphasage entre les deux sources. En P, le champ résultant total est donc:

L'onde résultante en P s'exprime donc comme le produit d'une fonction oscillante qui traduit le caractère ondulatoire de l'onde résultante, et d'une amplitude généralisée. Cette amplitude généralisée fait apparaître , qui est le déphasage entre la seconde et la première onde au point P, c'est-à-dire la différence entre la phase de l'onde 2 en P et la phase de l'onde 1 en P. Ces phases résultent de la propagation des ondes sur des distances données (les termes en k.ri), et des phases des sources elles-mêmes (ici, uniquement). Le déphasage est une fonction de l'espace, mais pas du temps.

Lorsque le déphasage vaut un multiple impair de pi,
          - : les ondes interfèrent de manière destructive. C'est le cas en P2.
Si par contre le déphasage vaut un multiple pair de pi,
          - : les ondes interfèrent de manière constructive. C'est le cas en P1.

L'intensité, qui est proportionnelle au carré de l'amplitude, c'est-à-dire à ,
          - est nulle pour les points auxquels les ondes interfèrent de manière destructive;
          - est proportionnelle à 4.A^2 là où les ondes interfèrent de manière constructive
            (ce qui est 2 fois la somme des intensités de chaque onde, A^2 + A^2 = 2.A^2).
(dans ces équations, x^2 signifie le carré de x).

Si les deux sources sont en phase (), le déphasage en P s'écrit , ce qui permet d'écrire les conditions précédentes de la façon suivante:

Si les deux sources émettent en phase (et uniquement dans ce cas),

  • lorsque la différence de chemin (r2-r1) vaut un multiple impair de /2,
              - (r2-r1) = (n + 1/2). : les ondes interfèrent de manière destructive.
                 Les maxima de l'une se superposent aux minima de l'autre.
  • lorsque la différence de chemin (r2-r1) vaut un multiple pair de /2,
              -     (r2-r1) = n. : les ondes interfèrent de manière constructive.
                Les maxima de l'une se superposent aux maxima de l'autre.

Si tout ceci est clair pour vous, passez à la page suivante, qui examine comment résoudre qualitativement un problème d'interférence.

Page précédente     Page suivante

Responsable du contenu et réalisation technique : Alain Jonas, UCLouvain