Dans certains cas, il faut non seulement identifier les conditions d'interférence constructive ou destructive, mais aussi calculer l'intensité de l'onde résultante à différents points de l'espace. Ceci est évidemment plus difficile que ce que nous avons fait jusqu'ici, puisqu'il faut additionner les champs, puis calculer l'intensité de l'onde résultante en évaluant la norme du vecteur de Poynting EXH moyenné sur une durée beaucoup plus grande que la période... (pour rappel, l'intensité d'une onde est le flux moyen d'énergie passant par unité de surface dans la direction de propagation de l'onde).

Pour simplifier le calcul, il est utile de passer à une représentation différente des ondes sinusoïdales, une représentation sous forme complexe. Considérons une onde électromagnétique de la forme (il est toujours possible de l'écrire localement sous cette forme, en choisissant correctement son repère; si l'onde est sphérique, A est une fonction de la distance à la source, x, mesurée le long d'un rayon; si l'onde est plane, A est une constante). Il est évident que nous pouvons aussi écrire:

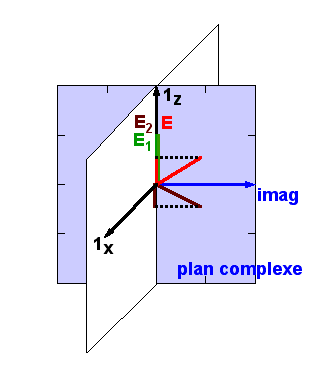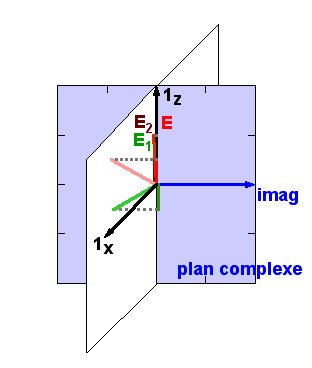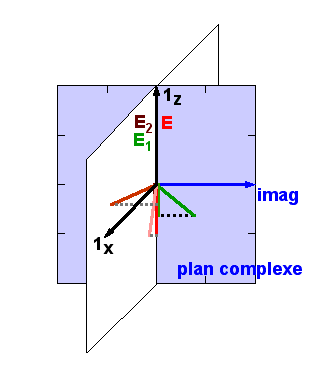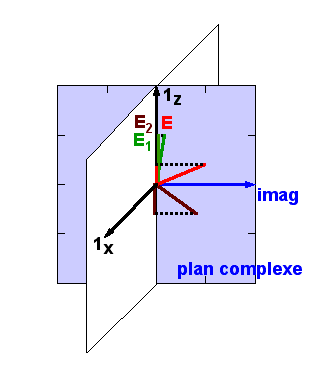
où Re{c} désigne la partie réelle d'un nombre complexe et j est la racine carrée de -1. Ecrire l'onde E sous cette forme revient en fait à la considérer comme la projection sur l'axe réel d'un champ complexe Ec tournant dans un plan imaginaire sans existence physique. Ceci est illustré ci-dessous en un point donné de l'espace: le plan bleu n'existe pas dans notre réalité, il est purement imaginaire et est colorié en bleu puisqu'il est du même domaine que vos rêves...

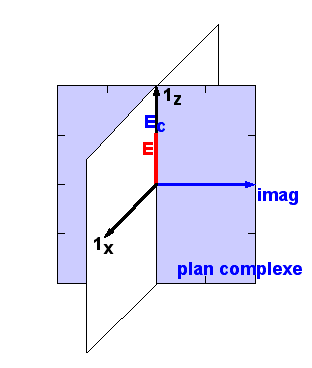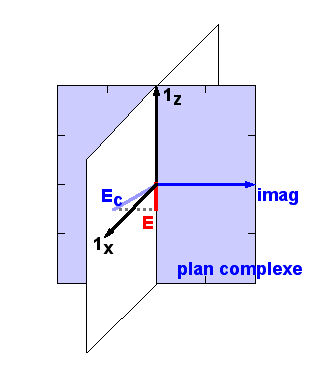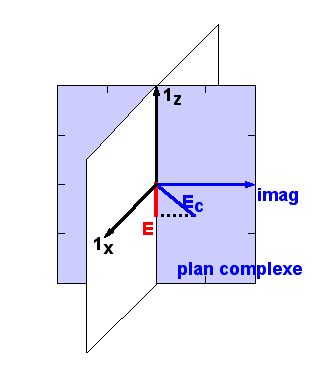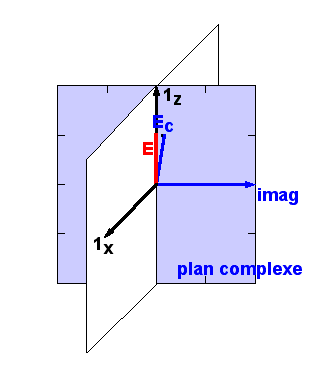
Comme la fonction Re{ } est linéaire, on peut très bien travailler dans un problème d'interférence avec les champs complexes tournants, les additionner, et prendre la partie réelle du total à la fin du calcul. Dans ce cas, on oublie en général que le champ électrique est réel, on le remplace par son expression complexe, et ce n'est qu'en bout de course qu'on se rappelle qu'il faut en prendre la partie réelle.

Qu'a-t-on gagné si ce n'est des ennuis, vous demandez-vous? Au moins deux choses. Tout d'abord, il est souvent plus facile d'additionner des exponentielles complexes que des cosinus. En effet, il est en général plus simple de mettre des facteurs communs en évidence avec des exponentielles. Mais ce n'est pas la raison essentielle de notre nouvelle notation. Si nous voulons calculer l'intensité du champ, il nous suffit maintenant de prendre le produit scalaire du champ complexe et de son complexe conjugué (à un facteur multiplicatif près). En effet, l'intensité de l'onde est proportionnelle au carré de l'amplitude du champ électrique, A^2. C'est exactement ce qu'on obtient en calculant:

L'intensité est donc bien proportionnelle à ce produit scalaire, la constante de proportionnalité étant comme indiqué dans la formule (32.29) de votre livre de référence (33.26 de l'ancienne édition).

De plus, vous verrez (peut-être) plus tard que cette notation complexe facilite le calcul des phénomènes ondulatoires dans des milieux absorbants ou conducteurs. Enfin, dans la troisième partie du cours (physique quantique), vous verrez qu'à toute particule matérielle est associée une onde complexe appelée "fonction d'onde", dont le carré de la norme (autrement dit l'intensité) donne la probabilité de présence de la particule à un endroit donné de l'espace. Les champs complexes que nous venons d'associer aux ondes électromagnétiques peuvent alors être considérés grosso-modo comme les fonctions d'onde des photons qui constituent l'onde.

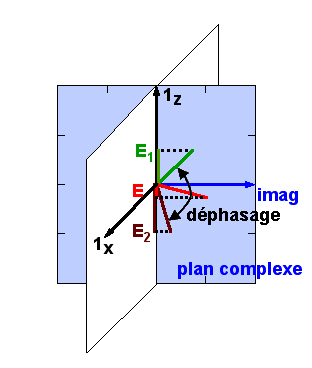
Graphiquement, voici à quoi ressemble la somme de deux ondes représentées par leurs vecteurs tournants, E = E1 + E2, dont l'une est en avance par rapport à l'autre (l'angle formé entre les deux vecteurs tournants est le déphasage angulaire) :

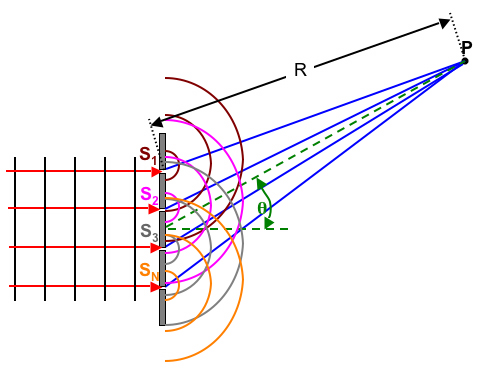
Utilisons à présent ce formalisme pour résoudre quantitativement un problème d'interférence. Un écran percé de N fentes infiniment étroites séparées les unes des autres par la distance d, est illuminé par une onde plane arrivant sous incidence normale (voir dessin ci-dessous).

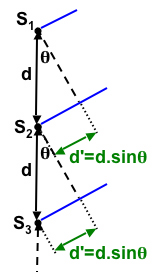On se place dans l'approximation de Fraunhofer, pour laquelle le point P où l'on veut calculer l'intensité se trouve très loin de l'écran. Comme précédemment, on peut alors considérer que les faisceaux bleus sont pratiquement parallèles. Chaque faisceau accuse un retard d' par rapport au faisceau supérieur voisin, comme illustré ci-contre. La distance entre la p-ième fente (ou source Sp) et le point P est R + (p-1).d'. Au point P, la superposition des faisceaux donne : Cette expression est simplement la somme des N ondes sphériques émises par chaque fente, avec un repère placé de telle sorte que les champs soient parallèles à 1z en P. Le symbole k est comme toujours le nombre d'onde, 2.pi divisé par la longueur d'onde. Evidemment, le champ électrique correspond seulement à la partie réelle de cette expression, mais par souci de simplicité nous admettons que le symbole Re{ } est implicite dans ce qui suit.

Maintenant, la seule chose qui reste à faire est un développement mathématique de cette expression. Tout d'abord, l'approximation de Fraunhofer implique que d' << R. Dans ce cas, on peut considérer que les préfacteurs des exponentielles sont pratiquement identiques. Notez que cette approximation n'est pas valide dans l'argument des exponentielles, puisqu'une différence d'une demi-longueur d'onde est évidemment très importante quand il s'agit d'additionner des cosinus (ou des exponentielles complexes). On écrit alors:

Ces calculs sont de simples opérations algébriques que vous vérifierez sans difficulté. La seule chose à se rappeler est l'expression de la série suivante (mentionnée dans toutes les tables de mathématiques):

A partir de là, il est aisé de calculer l'intensité de l'onde résultante en P :

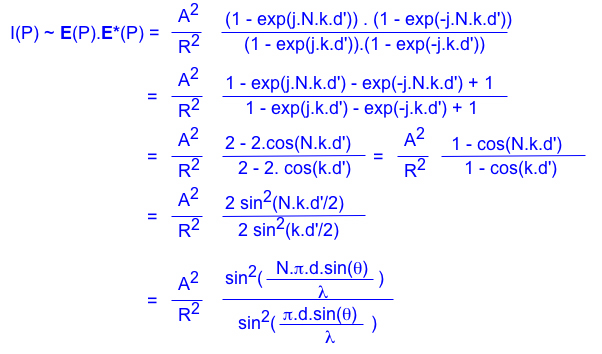
Cette expression montre que l'intensité diminue en fonction du carré de la distance entre les fentes et le point P (on s'en serait douté!). De plus, le numérateur passe régulièrement par zéro, chaque fois que vaut un multiple de pi, c'est-à dire quand où m est un nombre entier. Ces conditions correspondent en général à des situations dans lesquelles les ondes interfèrent globalement de manière destructive, sauf pour une série de cas particuliers. Ces cas particuliers correspondent aux conditions , où n est un autre nombre entier. Si cette condition supplémentaire est vérifiée, le dénominateur de l'expression précédente tend vers zéro également, et la limite du quotient tend vers N^2. L'intensité est alors (N.A/R)^2, et les ondes interfèrent toutes ensemble de manière constructive en P. Plutôt qu'un grand discours, examinez la figure ci-dessous qui représente graphiquement l'intensité pour 10 fentes.

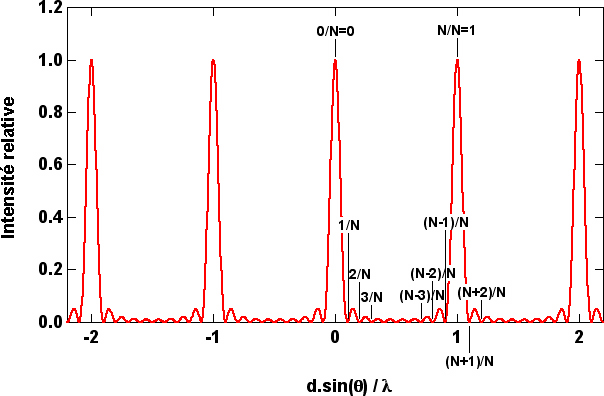
Vous voyez qu'il y a un grand nombre de possibilités de combiner les différents faisceaux pour arriver à une intensité nulle, tandis que les cas correspondant à l'interférence constructive de tous les faisceaux sont plus rares. Il y a encore beaucoup de choses à dire sur l'expression de l'intensité, mais vous pourrez sûrement faire vous-même les graphes correspondant à différents N ou à différentes longueurs d'onde, par exemple. Sachez enfin que nous avons considéré des fentes infiniment étroites; en général, il faut prendre en compte une largeur finie de fente, et un facteur supplémentaire s'introduit dans les expressions...

Page précédente