Si la longueur d'onde, la vitesse et la direction de propagation de l'onde changent lorsqu'elle est réfractée, qu'en est-il de sa polarisation? Et que se passe-t-il pour l'onde réfléchie? La question est un peu plus difficile et n'a été résolue qu'au 19ème siècle par Fresnel (sur base de concepts erronés, soit dit en passant). Comme pour le cas de la corde, il faut écrire des équations de continuité à l'interface. Ces équations, vous les avez vues pour le cas statique l'année passée. Elles sont toujours valables pour les champs électromagnétiques oscillants.
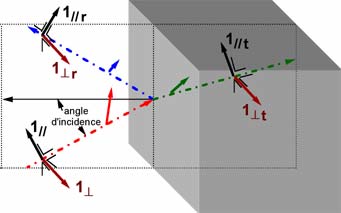
Pour les écrire, il faut choisir des systèmes de coordonnées adéquats, qui permettent d'exprimer les champs. Pour le champ électrique, on choisit les repères donnés dans la figure ci-dessous. Le champ est décomposé en ses composantes parallèle et perpendiculaire au plan d'incidence. Remarquez que les repères sont différents pour les trois ondes, incidente, réfléchie et réfractée.

Sur base des équations de continuité issues des équations de Maxwell, et de ces repères, on calcule alors des coefficients de réflexion et de transmission. Mais attention! Ici, il y a deux coefficients de réflexion, un pour la composante parallèle au plan d'incidence, et un pour la composante perpendiculaire, et ils sont différents. Idem pour les coefficients de transmission. Pourquoi? Cela est démontré rigoureusement dans les notes de cours, mais vous pouvez le comprendre intuitivement, puisque les équations de continuité dérivées des équations de Maxwell sont différentes selon que les champs sont perpendiculaires ou parallèles à l'interface.
Résumons: il y a quatre coefficients importants. Les deux coefficients de réflexion décrivent le rapport entre les 2 composantes des amplitudes du champ électrique réfléchi et du champ électrique incident. Il y a un coefficient qui donne le rapport des composantes des champs parallèles au plan d'incidence, et un coefficient qui donne le rapport des composantes des champs perpendiculaires au plan d'incidence. De même, mutatis mutandi, pour les deux coefficients de transmission. Comme ces coefficients sont différents (surtout en ce qui concerne les coefficients de réflexion), cela provoque un changement de polarisation lors de la réflexion (surtout) et de la réfraction (un peu).
Quand une onde incidente est polarisée parallèlement ou perpendiculairement au plan d'incidence, l'onde réfléchie est de même polarisation (parallèle ou perpendiculaire). Idem pour l'onde transmise. Quand l'onde n'est pas polarisée selon une de ces deux directions, tout se passe comme si l'onde se décomposait en deux composantes, l'une parallèle et l'autre perpendiculaire au plan d'incidence. Chacune de ces composantes vit sa vie, avec ses propres coefficients de réflexion et de transmission. Puis les deux composantes réfléchies se recombinent pour former l'onde réfléchie résultante (et de même pour l'onde transmise). Bien sûr, dire que "tout se passe comme si", ne veut pas dire que cela se passe effectivement au niveau physique, mais simplement que cette façon de voir permet de rendre compte des observations.
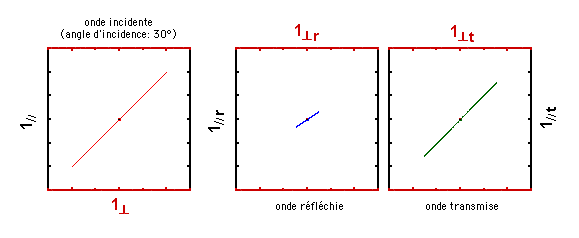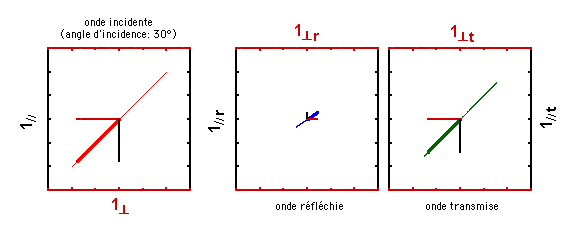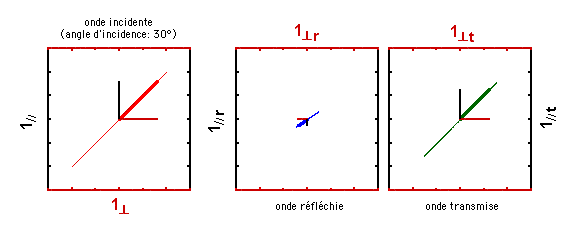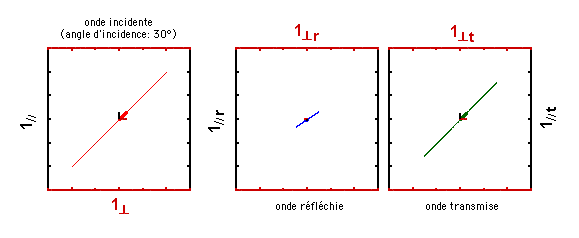
Voici ci-dessous une simulation des champs à l'interface entre de l'air et un verre d'indice de réfraction 1,5. L'onde incidente est polarisée linéairement, et le vecteur du champ incident est incliné à 45° par rapport au plan d'incidence. Pouvez-vous indiquer sur le dessin d'au-dessus où se trouve cet angle, qu'il ne faut pas confondre avec l'angle d'incidence bien sûr? Dans ce cas, les composantes du champ électrique incident sont identiques selon les deux vecteurs de référence choisis (voir la figure plus haut). L'angle d'incidence est de 30°. Que constatez-vous? Et pourquoi?
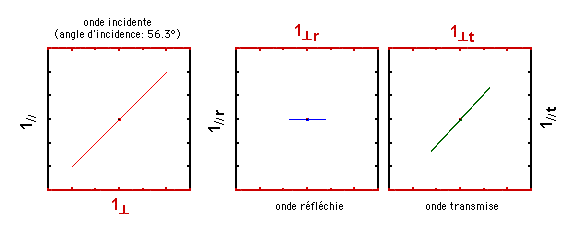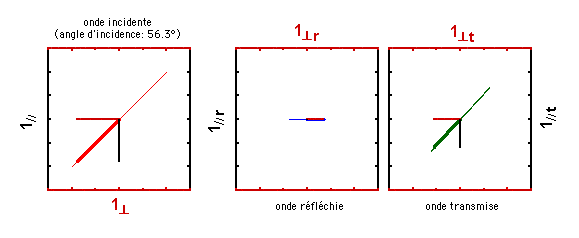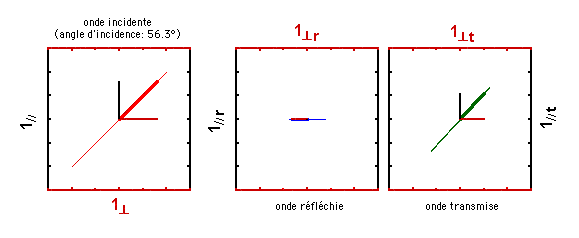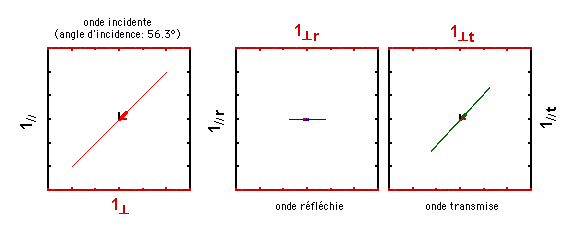
A présent, choisissons un angle d'incidence de 56.3°, un angle égal à l'arctangente de l'indice de réfraction du verre (1,5). Que constatez-vous? Comment s'appelle cet angle d'incidence particulier?
Pour une valeur d'angle d'incidence encore plus élevée (70°), voici ce qui se passe:
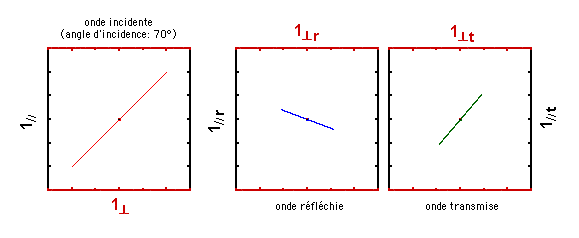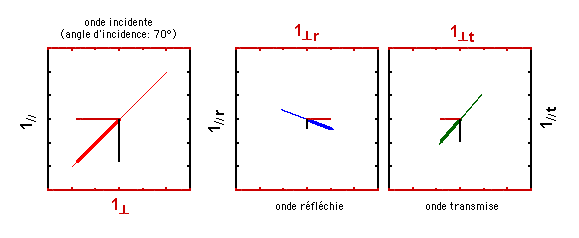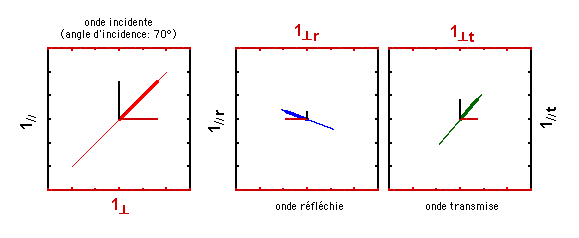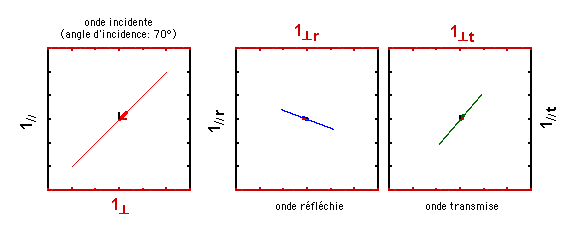
Ce comportement est formalisé dans vos notes de cours. Par ailleurs, vous aurez ou avez eu l'occasion de le mesurer au laboratoire. A la page suivante, on vous montre ce qui se passe si l'onde incidente est initialement polarisée de manière elliptique. Mais avant de passer à cette page, assurez-vous que vous avez bien compris ce que vous venez de voir.
Attention. Les équations de continuité à l'interface dépendent de la nature des matériaux de part et d'autre. Les équations dérivées dans le cours sont limitées au cas des matériaux isolants (on dit aussi diélectriques), non absorbants. Le verre, les polymères, l'air, les liquides organiques, l'eau désionisée, etc. sont de tels matériaux. Les équations doivent être modifiées pour prendre en compte le cas des matériaux conducteurs ou absorbants (métaux, semi-conducteurs,...), mais cela est trop compliqué pour ce cours d'introduction.