2. Un exemple très simple d'onde modulée en amplitude
Pour vous faire comprendre ce que signifie mathématiquement la modulation d'amplitude d'une onde, nous allons considérer un exemple très simple. Supposez que vous superposiez deux ondes planes monochromatiques de longueur d'onde et de fréquence légèrement différentes. Nous allons les suposer de même amplitude pour la facilité.
Le principe de superposition est d'application, et vous pourriez écrire que l'onde résultante vaut :
![]()
soit, en utilisant le fait que sin(a) + sin(b) = 2 sin( (a+b)/2 ) . cos( (a-b)/2 ),
![]()
Que signifie cette
expression? Elle montre que l'onde résultante peut être considérée
comme une onde porteuse de fréquence angulaire ( ![]() )/2, qui est proche de
)/2, qui est proche de ![]() et
de
et
de ![]() puisque nous les avons
elles-mêmes supposées proches. Mais l'amplitude de cette onde
n'est plus constante; l'amplitude s'exprime sous la forme d'un cosinus où
apparaissent les différences de fréquence et de longueur d'onde
des deux ondes initialement considérées. La porteuse
est donc modulée en amplitude par cette cosinusoïde qui joue le
rôle d'enveloppe délimitant les crêtes
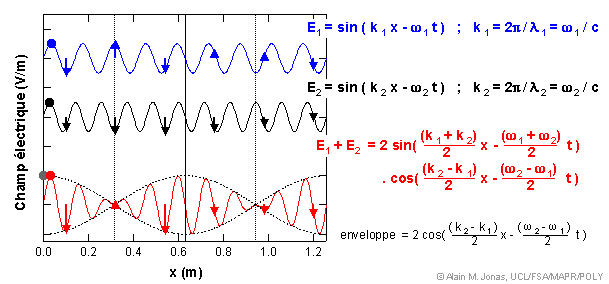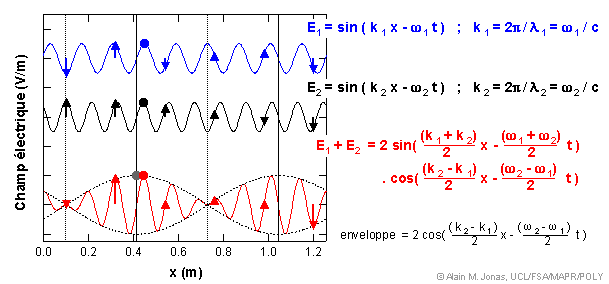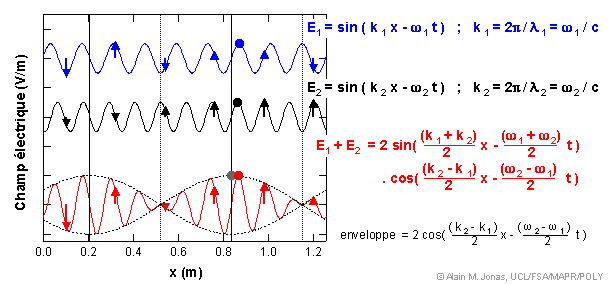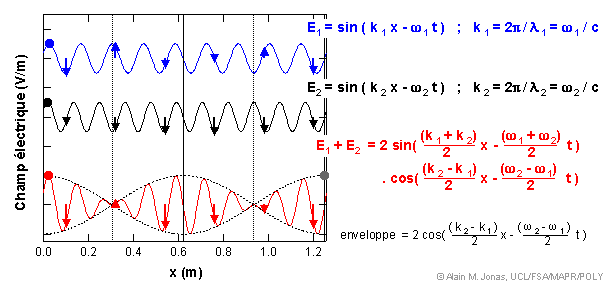
de la porteuse. Un graphique permet de mieux comprendre la situation:
puisque nous les avons
elles-mêmes supposées proches. Mais l'amplitude de cette onde
n'est plus constante; l'amplitude s'exprime sous la forme d'un cosinus où
apparaissent les différences de fréquence et de longueur d'onde
des deux ondes initialement considérées. La porteuse
est donc modulée en amplitude par cette cosinusoïde qui joue le
rôle d'enveloppe délimitant les crêtes
de la porteuse. Un graphique permet de mieux comprendre la situation:
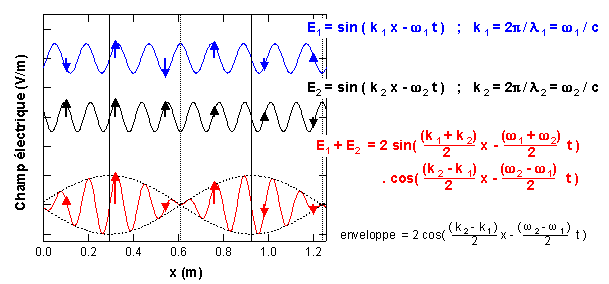
Sur cette image, les lignes noires verticales indiquent l'endroit où les deux ondes interfèrent de manière constructive. Les lignes pointillées correspondent aux endroits où les ondes interfèrent de manière destructive. Ces interférences se manifestent par l'apparition de l'enveloppe pointillée modulant la porteuse.
Peut-être pensez-vous que cela est simplement encore un autre exemple de figure d'interférence entre deux ondes. Vous avez raison. Mais il y a une différence importante par rapport aux interférences que vous avez étudiées jusqu'à présent, dans lesquelles les ondes étaient de même fréquence. Dans les cas précédents, parce que les ondes avaient même fréquence et longueur d'onde, les endroits où se produisaient les interférences constructives et destructives étaient fixes dans l'espace. Ici, ce n'est plus le cas. Regardez d'abord l'animation ci-dessous, qui vous donne un ralenti de la propagation des deux ondes et de leur résultante.
Vous voyez que les ventres et les noeuds de cette onde résultante se déplacent dans l'espace à une certaine vitesse. Cette conclusion pouvait facilement être obtenue à partir de l'équation de l'enveloppe de modulation. En effet, cette équation peut s'écrire sous la forme d'une solution de l'équation d'onde, f( x - vg.t ) :
![]()
L'enveloppe se propage donc comme une onde à la vitesse :
![]()
appelée vitesse de groupe (puisqu'elle donne la vitesse de déplacement d'un pulse). Cette vitesse est celle du gros point gris tracé sur l'animation. Comme vous pouvez le voir facilement sur cette animation, cette vitesse de groupe est dans le cas présent la même que la vitesse de déplacement d'un maximum de la porteuse, que l'on appelle vitesse de phase (qui est celle du gros point rouge tracé sur le diagramme animé). Ceci est logique, puisque le facteur représentant la porteuse est aussi une solution de l'équation d'onde, qui peut s'écrire sous la forme f( x -vp.t ) :
![]()
La vitesse de phase est donc de :
![]()
Dans le cas ici
considéré, on sait que la fréquence angulaire est liée
au nombre d'onde par la relation ![]() ,
où c est la vitesse de l'onde. A partir de cette relation, vous pourrez
établir très facilement (faites-le!) que vg
= vp = c, et que ces vitesses sont aussi celles des ondes
E1 et E2 (identiques à celles
des gros points bleus et noirs sur l'animation précédente). Dans
ce cas, vous pourriez vous demander pourquoi s'embarrasser des concepts de vitesse
de groupe et de phase; toutes les vitesses sont égales à c! La
réponse à votre question se trouve dans la section suivante. Avant
de l'aborder, assurez-vous que vous avez bien compris ce que
vous avez lu jusqu'ici.
,
où c est la vitesse de l'onde. A partir de cette relation, vous pourrez
établir très facilement (faites-le!) que vg
= vp = c, et que ces vitesses sont aussi celles des ondes
E1 et E2 (identiques à celles
des gros points bleus et noirs sur l'animation précédente). Dans
ce cas, vous pourriez vous demander pourquoi s'embarrasser des concepts de vitesse
de groupe et de phase; toutes les vitesses sont égales à c! La
réponse à votre question se trouve dans la section suivante. Avant
de l'aborder, assurez-vous que vous avez bien compris ce que
vous avez lu jusqu'ici.