|
|
|
Lecture 1, Monday, Sept. 14 |
Course overview, Finite element meshes, state
of the art, examples
Triangulations, Euler's formula, convex hull
Some notes for lectures 1,2 and 3
|
 |
Lecture 2, Monday, Sept. 21 |
Voronoi Diagram (2D)
Delaunay Triangulation (2D)
Delaunay Edges (global and local)
Edge Flip
|
 |
Lecture 3, Monday, Sept. 28 |
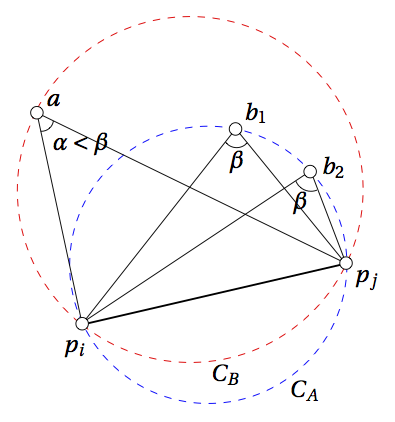
Delaunay Triagulation (continued)
The flip algorithm
Triangulations are flip connected
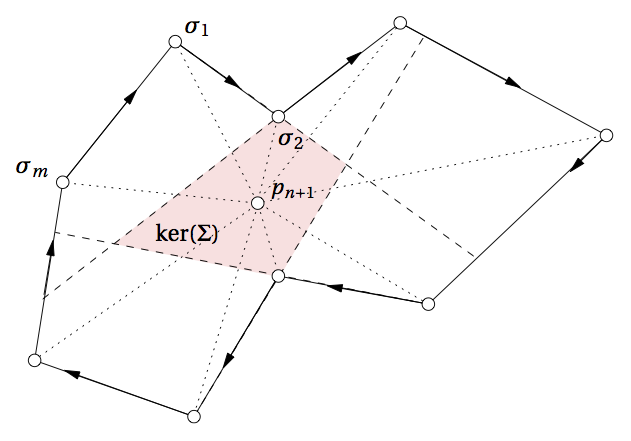
The Delaunay Kernel
Towards a O(n log n) algorithm
|
 |
Lecture 4, Monday, Oct. 5 |
Delaunay Triangulation in O(n log n)
Datastructures
Point sorting
Robust geometrical predicates
More reading: Robust Predicates .
|
 |
Lecture 5, Monday, Oct. 12 |
Delaunay Triangulation in O(n log n)
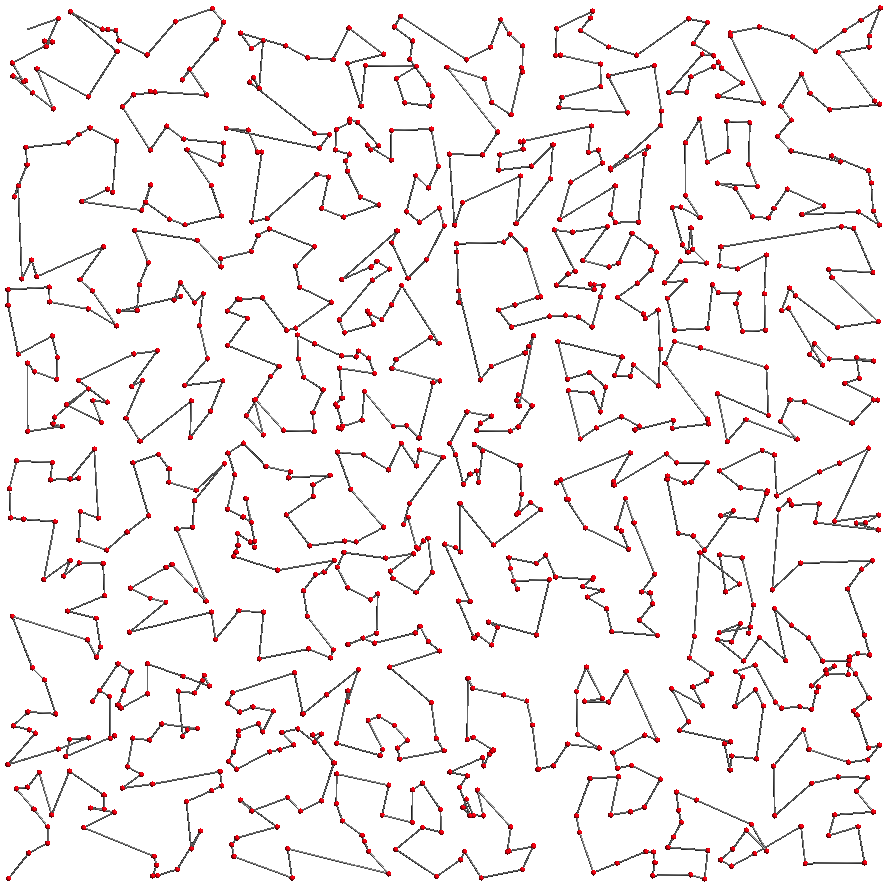
Space Filling Curves
Sorting points using the Hilbert Curve
Some notes on Delaunay Kernel
More reading: Hilbert curves
|
 |
Lecture 6, Monday, Oct. 19 |
Triangle Quality
The famous angle condition
Interpolation theory (Bramble-Hilbert)
Triangle quality
Some notes
|
 |
Lecture 7, Monday, Oct. 26 |
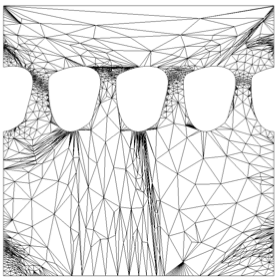
Mesh generation in 2D
Delaunay refinement
Frontal algorithms
|
 |
Lecture 10, Monday, Nov. 23 |
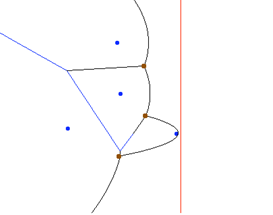
Fortune's algorithm
The famous Fortune's algorithm for generating 2D Voronoi diagrams
Some slides
|
 |
Lecture 11, Monday, Nov. 30 |
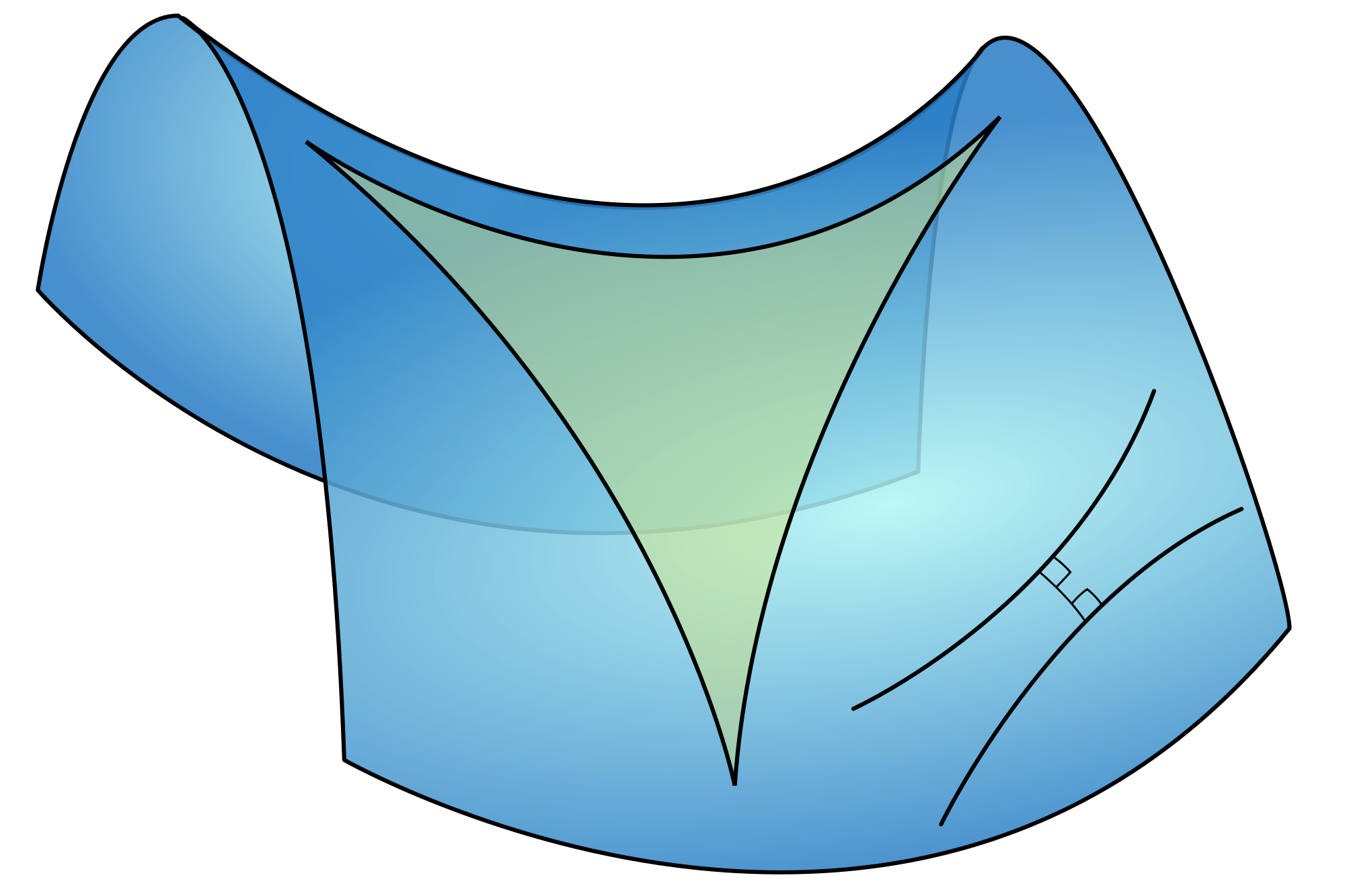
Differential Geometry
Differential geometry of curves (Frenet Frame, curvature, torsion)
Differential geometry of surfaces (Fundamental forms,
classifications of mappings, atlases...)
Some slides
|
 |
Lecture 12, Monday, Dec. 7 |
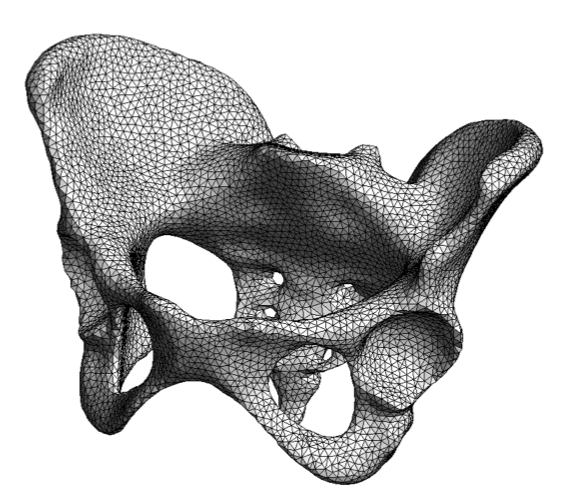
Harmonic maps
High quality surface meshing using harmonic maps
Some slides
|
 |