ERC Consolidator Grant

Learning to Control

Smart and Data-Driven Formal Methods for Cyber-Physical Systems control

The engineered systems surrounding us are increasingly hard to control. Not only the complicated interaction of the physical processes with the machines that control them, but also specifications (cyber-security, safety, privacy, resilience, resource-efficiency, decentralization) are more and more complex, and critical. Last but not least, in an increasing number of situations, no model of the system is available (or the model is too complex), and one needs to learn the optimal way of controlling the system by the mere observation of data.Our technological world is living a paradigm shift, which is often coined as the Cyber-Physical Revolution, or the Industry 4.0.

In view of these specificities, the only sensible way of controlling these complex systems is often by discretizing the different variables, thus transforming the model into a simple combinatorial problem on a finite-state automaton, called an abstraction of this system.  Until now, this approach has not been proved useful beyond small academic examples as it scales very poorly.

The goal of L2C is to transform this approach into an effective, scalable, cutting-edge technology that will address the CPS challenges and unlock their potential. This ambitious goal will be achieved by leveraging powerful tools from Mathematical Engineering. Out of this research, a state-of-the-art software platform will promote our results and translate them into directly usable solutions for the scientific and industrial communities.

L2Cis a pluri-disciplinary project at the frontier between Control Engineering, Computer Science and Applied Mathematics. It bridges the gap between rich innovative techniques and emerging challenges in Control. It impacts both fundamental Science and Engineering, as the theoretical research is driven and fostered by cutting edge technological challenges.

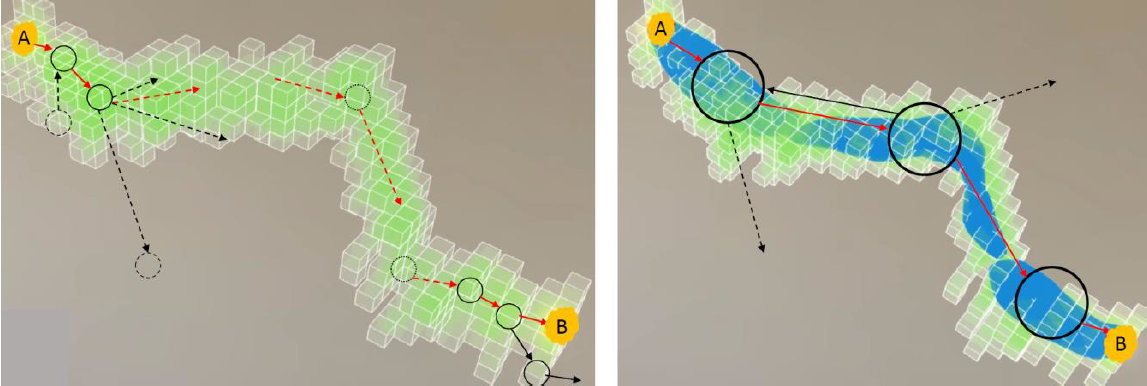
Smart abstraction approach: instead of discretizing the state-space into a huge number of similar infinitesimally small cells, we aim at subdividing the state-space into smartly computed, macroscopic, regions.

Smart abstraction approach: co-designing the abstraction and controller to reduce the part of the abstraction built for an optimal reachability control problem.

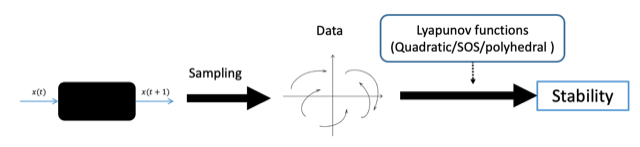
Data-driven stability analysis

A (probabilistic) path-complete graph, and its (product and path) lifts used to refine the analysis

Code

Dionysos is the software of the ERC project Learning to control (L2C). In view of the Cyber-Physical Revolution, the only sensible way of controlling these complex systems is often by discretizing the different variables, thus transforming the model into a simple combinatorial problem on a finite-state automaton, called an abstraction of this system. The goal of L2C is to transform this approach into an effective, scalable, cutting-edge technology that will address the CPS challenges and unlock their potential. This ambitious goal will be achieved by leveraging powerful tools from Mathematical Engineering.

Code available on Github

Materials

Our team

Publications

• Debauche, V., Della Rossa, M., & Jungers, R. M. (2021). Comparison of Path-Complete Lyapunov Functions via Template-Dependent Lifts. arXiv preprint arXiv:2110.13474.
• Berger, G. O., Jungers, R. M., & Wang, Z. (2021, May). Chance-constrained quasi-convex optimization with application to data-driven switched systems control. In Learning for Dynamics and Control (pp. 571-583). PMLR.
• Legat, B., Jungers, R. M., & Bouchat, J. (2021, May). Abstraction-based branch and bound approach to Q-learning for hybrid optimal control. In Learning for Dynamics and Control (pp. 263-274). PMLR.
• Ren, W., Dimarogonas, D. V., & Jungers, R. (2021, June). Event-Triggered Tracking Control of Networked and Quantized Control Systems. In 2021 European Control Conference (ECC) (pp. 632-637). IEEE.
• Ren, W., Calbert, J., & Jungers, R. (2021). Zonotope-based Controller Synthesis for LTL Specifications. arXiv preprint arXiv:2108.00704.
• Aspeel, A., Rutledge, K., Jungers, R. M., Macq, B., & Özay, N. (2021). Optimal Control for Linear Networked Control Systems with Information Transmission Constraints. arXiv preprint arXiv:2109.10666.
• Wang, Z., Berger, G. O., & Jungers, R. M. (2021). Data-driven feedback stabilization of switched linear systems with probabilistic stability guarantees. arXiv preprint arXiv:2103.10823.
• Della Rossa, M., Wang, Z., Egidio, L. N., & Jungers, R. M. (2021). Data-driven stability analysis of switched affine systems. arXiv preprint arXiv:2109.11169.
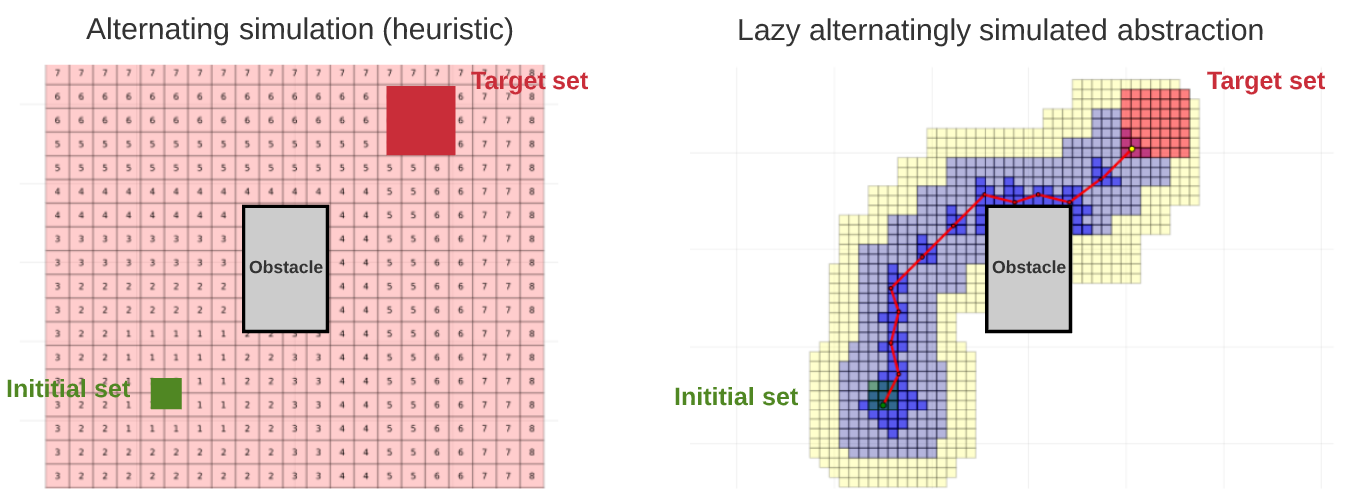
• Calbert, J., Legat, B., Egidio, L. N., & Jungers, R. (2021, December). Alternating simulation on hierarchical abstractions. In 2021 60th IEEE Conference on Decision and Control (CDC) (pp. 593-598). IEEE.
• Debauche, V., Della Rossa, M., & Jungers, R. M. (2021). Template-Dependent Lifts for Path-Complete Stability Criteria and Application to Positive Switching Systems. IFAC-PapersOnLine, 54(5), 151-156.
• Ren, W., Vlahakis, E., Athanasopoulos, N., & Jungers, R. (2021). Optimal Resource Scheduling and Allocation in Distributed Computing Systems. arXiv preprint arXiv:2112.00708.
• Aspeel, A., Gouverneur, A., Jungers, R. M., & Benoît, M. A. C. Q. (2020, October). Optimal measurement budget allocation for particle filtering. In 2020 IEEE International Conference on Image Processing (ICIP) (pp. 1-5). IEEE.